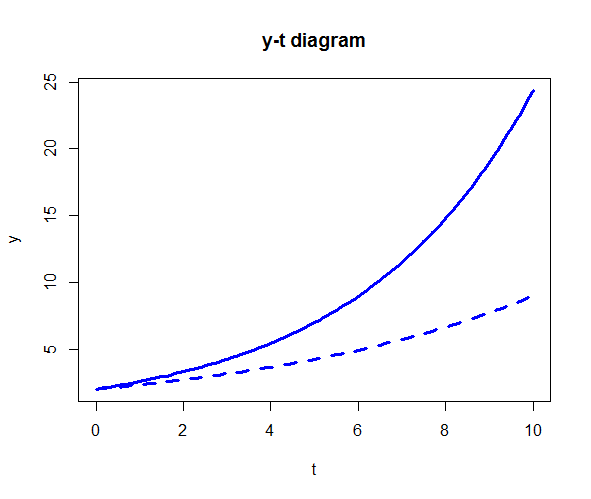
Twee oplossingskrommen in één diagram We bekijken het exponentiële groeimodel \[\frac{\dd y}{\dd t}=r\cdot y\] bij twee verschillende relatieve groeisnelheden \(r\). Onderstaand R script

library("deSolve")

model <- function(tijd, begintoestand, parameters) {
  with(as.list(c(begintoestand, parameters)), {
    dydt <- r*y
    return(list(dydt))
  })
}

params1 <- c(r = 0.25)    # relatieve groeisnelheidsconstante
params2 <- c(r = 0.15)    # idem
y <- c(y=2)               # beginwaarden
t <- seq(0, 10, by = 0.1) # tijdsinterval

oplossing1 <- ode(y, t, model, params1)
oplossing2 <- ode(y, t, model, params2)

plot(oplossing1, oplossing2,
     main = "y-t diagram", xlab = "t", ylab="y", 
     lwd = 3, col = "blue"
)

levert onderstaande figuur op.

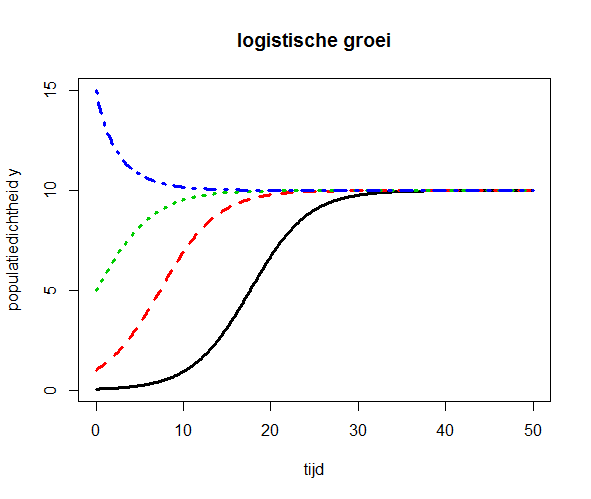
Meerdere oplossingskrommen in één diagram We bekijken het logistische groeimodel \[\frac{dy}{dt}=r\cdot y\cdot(1-y/K)\] bij meerdere beginwaarden \(y_0\). Onderstaand R script

library(deSolve)

model <- function(tijd, begintoestand, parameters) {
  with(as.list(c(begintoestand, parameters)), {
    dydt <- r*y*(1-y/K)
    return(list(dydt))
  })
}

y0 <- c(y = 0.05) # populatiedichtheid aan het begin
params  <- c(r = 0.3, # relatieve groeisnelheidsconstante
             K = 10)  # draagkracht
t <- seq(from = 0, to = 50, by = 0.1) # tijdsinterval


oplossing <- ode(y0, t, model, params)

# nog meer beginwaarden
y0s <- cbind(y = c(1, 5, 15))  
oplossingen <- list()
for (i in 1:nrow(y0s)) {
  oplossingen[[i]] <- ode(y0s[i,], t, model, params)
}

plot(oplossing, oplossingen, 
     main = "logistische groei", 
     xlab = "tijd", ylab="populatiedichtheid y", 
     lwd = 3)

levert onderstaande figuur op.