Doing mathematics with R: Differential equations in R
 Solving systems of differential equations
Solving systems of differential equations
You can also easily solve systems of differential equations numerically in R. The following example of a system of linear differential equations in two dependent variables illustrates how, but it is not so different from one dependent variable. Only we will also show you how to zoom in on a part of the graph.
System of linear GDVs Consider the following system of differential equations \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= a\cdot x+b\cdot y \\[0.25cm] \frac{\dd y}{\dd t} &=c\cdot x+d\cdot y\end{aligned} \right.\] with \[a=2,\quad b=-4,\quad c=2,\quad d=-3\] and initial values \[x(0)=2,\quad y(0)=3\]
The R script below
library(deSolve)
model <- function(time, initialstate, parameters) {
with(as.list(c(initialstate, parameters)), {
dxdt <- a*x + b*y
dydt <- c*x + d*y
return(list(c(dxdt, dydt)))
})
}
params <- c(a = 2, b = -4, c = 2, d = -3) # parameters
xy0 <- c(x = 2, y = 3) # initial values
t <- seq(0, 10, by = 0.1) # time interval
solution <- ode(xy0, t, model, params)
plot(solution, main = c("x-t diagram", "y-t diagram"),
xlab = "t", ylab = c("x", "y"), lwd = 2, col = "blue")
plot(solution[, "x"], solution[, "y"], type = "l",
main = "y versus x", xlab = "x", ylab = "y",
lwd = 2, col = "blue")
xy <- subset(solution, select = c("x", "y"),
subset = -1<x & x<1 & -1<y & y<1)
plot(xy, type = "l", main = "y versus x",
xlab = "x", ylab = "y", lwd=2, col = "blue")yields the following diagrams
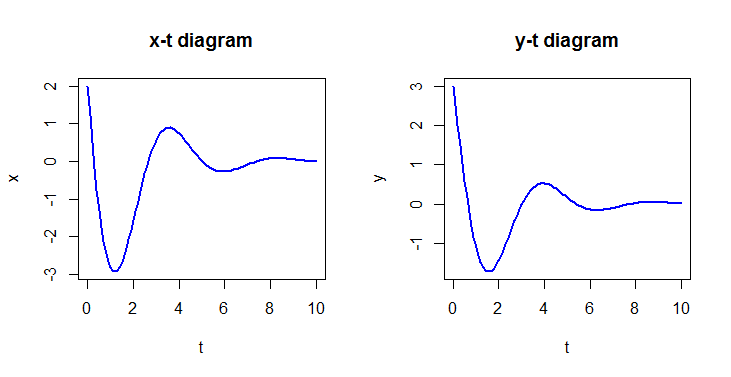
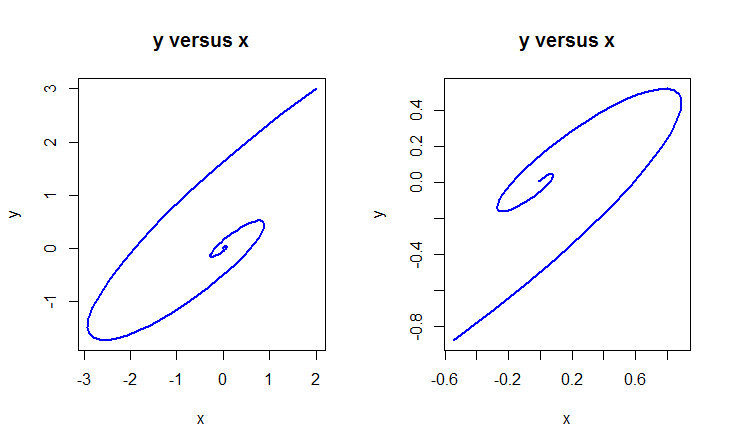
Unlock full access



