Werken met R bij wiskunde: Differentiaalvergelijkingen in R
 Parameterschatting bij differentiaalvergelijkingen
Parameterschatting bij differentiaalvergelijkingen
We hebben al eerder gezien hoe via regressieanalyse parameterwaarden geoptimaliseerd kunnen worden bij expliciete oplossingen van differentiaalvergelijkingen. Het FME pakket met zijn afhankelijke R pakketten stelt de gebruiker ook in staat om parameters in differentiaalvergelijkingen te fitten aan meetgegevens. We geven een voorbeeld van kwantitatieve farmacokinetiek, namelijk dat van orale toediening van een medicament dat vervolgens geëlimineerd wordt uit het menselijk lichaam.
Orale toediening van een farmacon met eerste-orde kinetiek van absorptie en eliminatie Propranolol is een bètablokker die onder meer gebruikt wordt voor het verlagen van de bloeddruk. Bij orale toediening, d.w.z. het slikken van tabletten of het nuttigen van medicinale drank, komt het medicijn eerst in de maag terecht. Met enige vertraging komt het farmacon vervolgens in de dunne darm; de vertraging is in een concentratie-tijdkromme te zien doordat de concentratie pas een tijdje (\(t_\text{lag}\)) na orale toediening begint te stijgen. Vanuit de dunne darm komt het farmacon d.m.v. een diffusieproces via de poortader in de lever terecht. Het absorptieproces volgt in deze stap voornamelijk eerste-orde kinetiek vanwege passieve diffusie. De lever laat echter maar een beperkt deel onveranderd doorgaan naar de algemene bloedcirculatie van het lichaam (voorbij de poortader en de lever). Via het bloed verspreidt het doorgelaten farmacon zich vervolgens verder over het lichaam en kan zijn therapeutische werking doen. De fractie van het toegediende farmacon dat onveranderd in de algemene bloedcirculatie terechtkomt wordt in de Nederlandse vakliteratuur de biologische beschikbaarheid van het farmacon genoemd.
Zodra het geabsorbeerde farmacon zich verdeeld over het lichaam (dit kan dus ook in verschillende weefsels en lichaamsvocht plaatsvinden) ondergaat het ook het proces van eliminatie. In het begin overstijgt de geabsorbeerde hoeveelheid de geëlimineerde met als gevolg dat de plasmaconcentratie stijgt. Op het maximum is de absorptie even groot als de eliminatie. Na verloop van tijd, wanneer het absorptieproces op zijn einde loopt, overheerst de eliminatie; de concentratie neemt dan af in de loop van de tijd. Onderstaande grafiek toont de typische vorm van concentratie-tijdkromme voor een oraal toegediend farmacon.
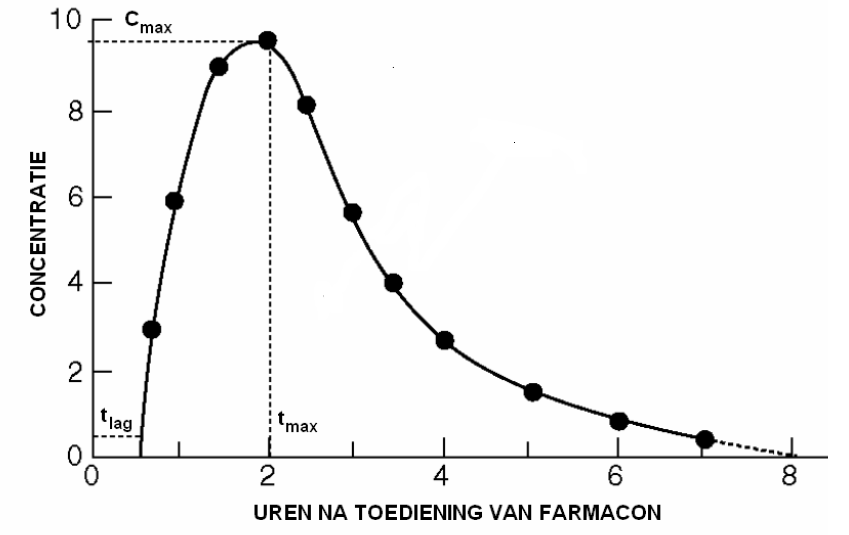
Bovenstaande krommen hoort bij een bi-exponentieel model, maar we kunnen het ook op een andere wijze beschrijven, namelijk als dynamisch systeem, Onderstaand diagram toont een grafische weergave van het model voor orale toediening van een farmacon met eerste-orde kinetiek voor absorptie in en eliminatie uit het lichaam, beschouwd als één centraal compartiment:

Dit plaatje stelt het volgende voor: uit de dunne darm wordt het farmacon geabsorbeerd en komt via de lever voor een deel in de algemene bloedcirculatie terecht. Voor de afname vanhet farmacon uit de dunne darm hanteren we een exponentieel model met eliminatiesnelheidsconstante \(k_a\). Dus: \[\frac{\dd A_\text{dunne darm}}{\dd t} = -k_a\cdot A_\text{dunne darm}\] waarbij \(A_\text{dunne darm}\) de hoeveelheid van het oraal toegediende farmacon in de dunne darm is. De snelheid waarmee dit in de algemene bloedcirculatie komt heeft tegengesteld teken en slechts een fractie van het farmacon passeert de dunne darm en lever. Dit verdisconteren we in de bijpassende toename aan de plasmaconcentratie \(C\) van het farmacon met een effectiviteitsconstante \(\mathrm{eff}\), die van de biologische beschikbaarheid en het verdelingsvolume afhangt. Samen met de eerste-orde kinetiek van eliminatie uit het lichaam kunnen we opschrijven in wiskundetaal: \[\frac{\dd C}{\dd t} = k_a\cdot \mathtt{eff}\cdot A_\text{dunne darm} -k_e\cdot C\] We hebben dus een stelsel van differentiaalvergelijkingen.
We fitten de drie parameters \(k_a\), \(k_e\) en \(\mathtt{eff}\) aan de hand van literatuurgegevens uit het volgende artikel
Olanoff, L.S., Walle, T., Cowart, T.D., Oexmann, M.J & Conradi, E.C. (1986). Food effects on propranolol systemic and oral clearance: support for a blood flow hypothesis. Clinical Pharmacology and Therapeutics, 40, 408-414.
Implementatie en paramterschatting in R Voor het gemak noteren we de hoeveelheid van propanolol in de dunne darm met \(x\) en de plasmaconcentratie met \(y\). We hebben dan te maken met het volgende stelsel van differentiaalvergelijkingen: \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &=-k_a\cdot x \\ \\ \frac{\dd y}{\dd t} &= k_a\cdot \mathtt{eff}\cdot x -k_e\cdot y\end{aligned}\right.\] Vanwege de parameterschatting gebruiken we het FME (Flexible Modelling Environment) pakket en zijn afhankelijke pakketten deSolve, rootSolve en coda. Een alternatief is het grind (GReat INtegrator Differential equations) pakket als gebruikersinterface tot de onderliggende R pakketten, maar we zullen dit niet bespreken.
Onderstaand R script gebruikt het ode command uit het deSolve pakket om bij geschatte parameterwaarden de oplossingskromme numeriek uit te rekenen. In het plot commando uit het pakket tekenen we de meetgegevens samen met de oplossingskromme in één figuur.
library("FME")
model <- function(tijd, begintoestand, parameters) {
with(as.list(c(begintoestand, parameters)), {
dxdt <- -ka * x
dydt <- ka *x * eff - ke * y
list(c(dxdt, dydt))
})
}
gegevens <- data.frame(
tijd = c(0.5, 1, 1.5, 2, 3, 5, 7, 9),
y = c(9.15, 44.82, 56.29, 51.33, 36.43,
22.89, 13.06, 7.21)
)
params <- c(ka = 2, ke = 0.3, eff = 1)
xy0 <- c(x = 80, y = 0)
t <- seq(from = 0.45, to = 10, by = 0.05)
oplossing <- ode(xy0, t, model, params)
plot(oplossing, obs = gegevens,
xlim = c(0,10), ylim = c(0,60),
main = "concentratie propanolol",
xlab = "tijd (u)", ylab = "y (µg/L)",
obspar = list(pch=16, col="red"))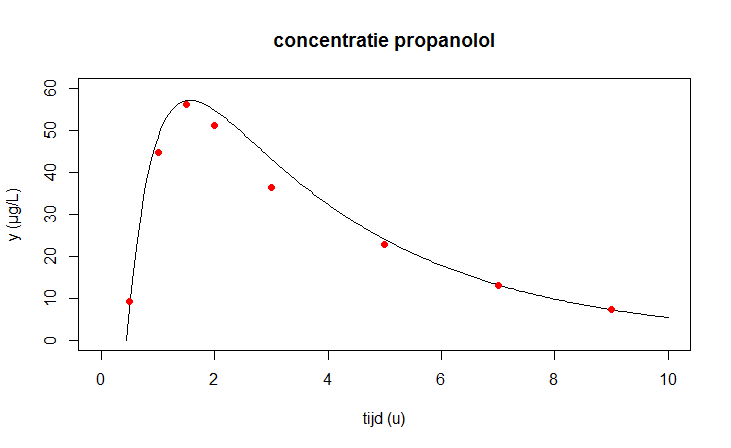
We hebben hier redelijke parameterwaarden geschat op basis van literatuurgegevens, maar we kunnen deze waarden ook gebruiken als startwaarden voor een stelselmatige verbetering van de modeluitkomsten in relatie tot de meetgegevens.
Hiervoor moeten een cost functie definiëren m.b.v. modCost om te schatten wat de residuele afwijking is tussen modelresultaten en meetgegevens.
cost <- function(p) {
opl <- ode(xy0, t, model, p)
dimnames(opl) <- list(NULL, c("tijd", "x", "y"))
modCost(opl, gegevens, x="tijd", weight = "none")
}Omdat we de Nederlandse naam "tijd" hebben gebruikt in de meetgegevens i.p.v. "time", moeten we in de numerieke oplossing van het stelsel differentiaalvergelijkingen bij zekere parameterwaarden het kopje met de naam "time" aanpassen en in het modCost commando ook aangeven dat de onafhankelijke variable "tijd" is.
Hierna kunnen we met het modFit commando bij zekere startwaarden tot betere parameterwaarden pogen te komen. Onderstaande code fragment
params <- c(ka = 2, ke = 0.3, eff = 1)
modelfit <- modFit(f = cost, p = params)
print(summary(modelfit))levert in het console venster een afdruk van betere parameterwaarden:
Parameters:
Estimate Std. Error t value Pr(>|t|)
ka 2.25216 0.31238 7.21 0.000800 ***
ke 0.29163 0.02684 10.87 0.000115 ***
eff 0.90873 0.04931 18.43 8.65e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
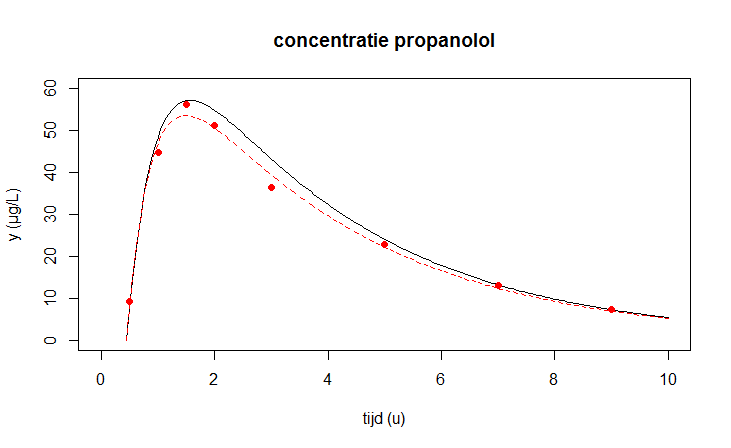
Residual standard error: 2.206 on 5 degrees of freedomTot slot tonen we in één figuur de eerder berekende modeluitkomsten en de verbeterde uitkomsten bij \(k_a=2.252\), \(k_e = 0.292\) en \(\text{eff}=0.909\).
opl1 <- ode(xy0, t, model, params)
opl2 <- ode(xy0, t, model, coef(modelfit))
plot(opl1, pl2, obs = gegevens,
xlim = c(0,10), ylim = c(0,60),
main = "concentratie propanolol",
xlab = "tijd (u)", ylab = "y (µg/L)",
obspar = list(pch=16, col="red")
)