Werken met R bij wiskunde: Differentiaalvergelijkingen in R
Differentiaalvergelijkingen met gebeurtenissen
In een model hoeven de modelvergelijkingen niet steeds hetzelfde te blijven. In een farmacokinetisch model met een voorschrift van dosering van een medicijn of bij regelsystemen zijn er gebeurtenissen ("events") die de vergelijkingen veranderen. Bij herhaalde intravenuze inspuitingen zijn er momenten waarop de concentratie van een farmacon abrupt omhoog gaat. In een natuurkundig voorbeeld van een stuiterende bal zal bij de botsing van de vallende bal op een horizontaal oppervlak abrupt de richting en de snelheid van de bal wijzigen. Een biomedisch voorbeeld van de laatste vorm van gebeurtenissen is een regelsysteem, waarin gebeurtenissen het gedrag van een systeem beïnvloeden: denk bijvoorbeeld aan het instand houden van de bloedsuikerspiegel in het menselijk lichaam, Dergelijke modellen kun je ook in deSolve pakket opstellen. We illustreren dit aan de hand van een 1-compartimentmodel van herhaalde intraveneuze inspuitingen, maar dit is ook toepasbaar bij een 2-compartimentmodel van herhaalde orale toediening van medicatie. Ook bekijken we een voorbeeld van populatiebeheer door vangst (of oogst, afhankelijk van de context; in het Engels wordt de naam "harvesting" gebruikt), waarbij op[ het moment dat een populatie een bepaalde omvang bereikt door vangst deze abrupt kleiner gemaakt wordt.
Model van herhaalde inspuitingen We bekijken een één-compartimentmodel met eerste-orde kinetiek voor eliminatie van het antibioticum Ceftazidim en een reeks van bolusinjecties met gelijke dosis die met regelmatige tussenpozen toegediend worden. Het doseringsinterval noteren we in het vervolg als \(\tau\). Realistische farmacokinetische parameterwaarden zijn een herhaalde dosis \(D=1000\,\text{mg}\), een eliminatieconstante \(k = 0.034\,\text{h}^{-1}\) en een verdelingsvolume \(V_d=20.6\,\text{L}\), waarmee je de plasmaconcentratie \(C\) van het farmacon kunt berekenen uit de hoeveelheid \(A\) van het farmacon in de bloedbaan via de formule \(C =A / V_d\). Deze gegevens komen uit een wetenschappelijk onderzoek bij patiënten die last hadden van chronische nierinsufficiëntie (M.A.Demotes-Mainard, F., Vincon, G., Ragnaud, J.M., Morlat, P., Bannwarth, B. & Dangoumau, J. (1993). Journal of Clinical Pharmacology, 33, 475-479). Farmacokinetische kengetallen voor medicijnen kun je ook vinden in informatieteksten die door het ‘College ter Beoordeling van Geneesmiddelen’ geregistreerd zijn; zie bijvoorbeeld de websites www.cbg-meb.nl en www.geneesmiddelenrepertorium.nl.
We geven twee implementaties in R, waarbij de tweede methode via gebeurtenissen de sterke voorkeur heeft omdat deze niet afhangt van de numerieke methode voor het oplossen van de differentiaalvergelijking en eigenlijk het gemakkelijkst is.
In dit farmacokinetische model geldt tussen de inspuitingen in \[\frac{\dd C}{\dd t}=-k\cdot C\] en na elk doseringsinterval \(\tau\) wanneer opnieuw een bolusinjectie plaatsvindt wordt de plasmaconcentratie abrupt ophoog met \(D/V_d\). Het computermodel kan niet abrupt te concentratie ophogen, maar we kunnen het wel zo inrichten dat na elke inspuiting in korte tijd, zeg in de tijdsduur \(\delta\), een lineaire toename in de plasmaconcentratie tot de gewenste ophoging leidt. Met ander woorden, we passen de functie die de afgeleide oplevert voor de oplossingsmethode aan.
Het volgende R script
library(deSolve)
delta <- 1/100
model <- function(tijd, begintoestand, parameters) {
with(as.list(c(begintoestand, parameters)), {
if (tijd %% tau <= delta) {
u <- (D/Vd)/ delta
} else {
u <- 0
}
dCdt <- -k*C + u
list(c(dCdt))
})
}
params <- c( k = 0.034, # eliminatieconstante
Vd = 20.6, # distributievolume
D = 1000, # dosis
tau = 24 # doseringsinterval
)
t <- seq(from = 0, to = 150, by = delta) # tijdsinterval
C0 <- c(C = 0) # beginwaarden
oplossing <- ode(C0, t, model, params)
plot(oplossing, type = "l", lwd = 2,
xlab = "tijd (u)", ylab = "C (mg/L)",
main = "plasmaconcentratie-tijd diagram")levert onderstaande grafiek op:
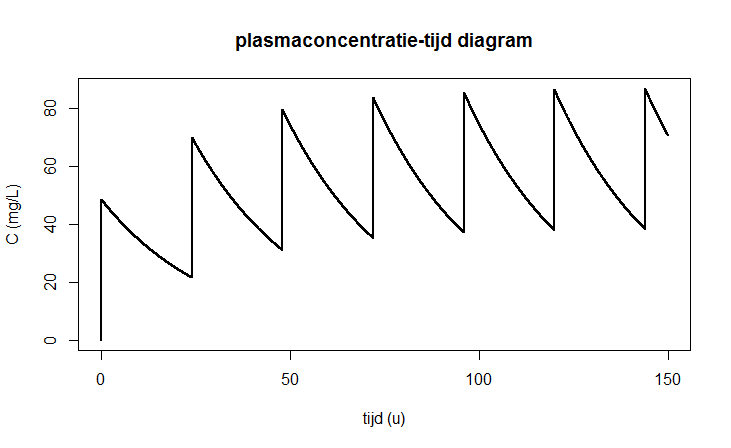
Bovenstaande implementatie hangt wel af van de methode waarop het stelsel opgelost wordt. Als je de Euler methode zou toepassen in het ode commando (via method="euler"), dan krijg je geen goede grafiek omdat bijvoorbeeld na 48 uur het interval van toediening van het farmacon niet goed herkend wordt:
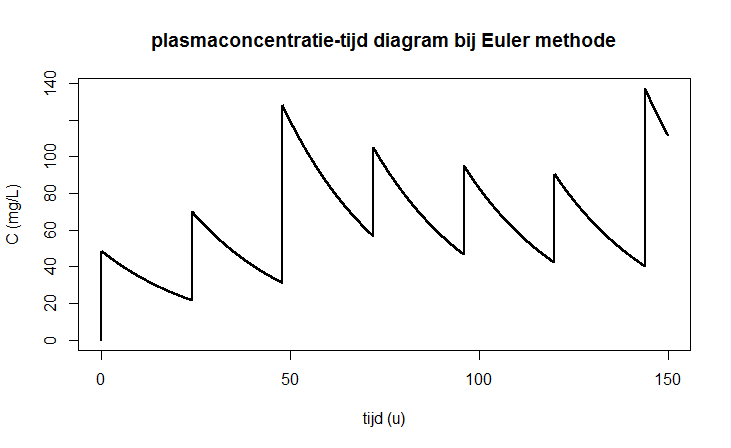
Implementatie in R via gebeurtenissen In dit farmacokinetische model geldt tussen de inspuitingen in \[\frac{\dd C}{\dd t}=-k\cdot C\] en na elk doseringsinterval \(\tau\) wanneer opnieuw een bolusinjectie plaatsvindt wordt de plasmaconcentratie abrupt ophoog met \(D/V_d\). We doen dit nu niet via de afgeleide, maar via de grootheid zelf. De inspuitingen worden via een speciale gebeurtenis gespecificeerd die op bekende tijdstippen plaatsvinden. In een dataframe specificeer je
- de naam van de toestandsvariabele die van waarde wijzigt;
- de tijdstippen waarop de eranderingen moeten plaatsvinden;
- de sterkte van de verandering;
- de aard van de verandering (replace, add, multiply).
Voor de rest specificeer je op de gewone manier hoe het model zich tussen de gebeurtenissen gedraagt en breng je in het ode commando de events optie ten tonele.
Het volgende R script
library(deSolve)
model <- function(tijd, begintoestand, parameters) {
with(as.list(c(begintoestand, parameters)), {
dCdt <- -k*C
list(c(dCdt))
})
}
params <- c(k = 0.034) # eliminatieconstante
D <- 1000 # dosis
Vd <- 20.6 # distributievolume
tau <- 24 # doseringsinterval
inspuitingen <- data.frame(var = "C",
time = seq(
from = 0,
to = 150,
by = tau),
value = D/Vd,
method = "add")
t <- seq(from = 0, to = 150, by = 1) # tijdsinterval
C0 <- c(C = 0) # beginwaarden
oplossing <- ode(C0, t, model, params,
events = list(data = inspuitingen))
plot(oplossing, type = "l", lwd = 2,
xlab = "tijd (u)", ylab = "C (mg/L)",
main = "plasmaconcentratie-tijd diagram")levert onderstaande grafiek op:
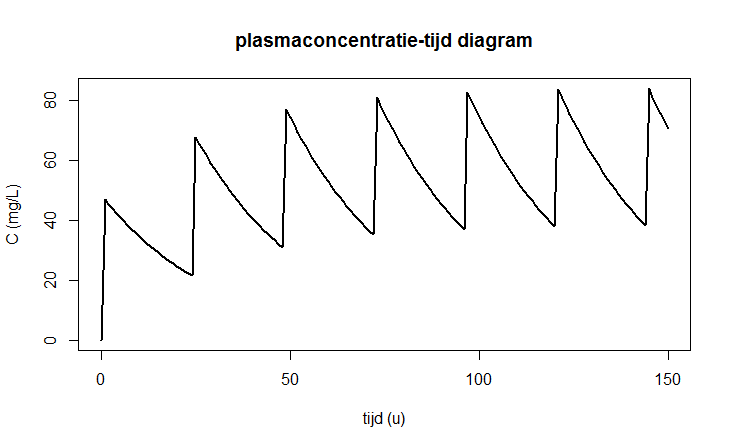
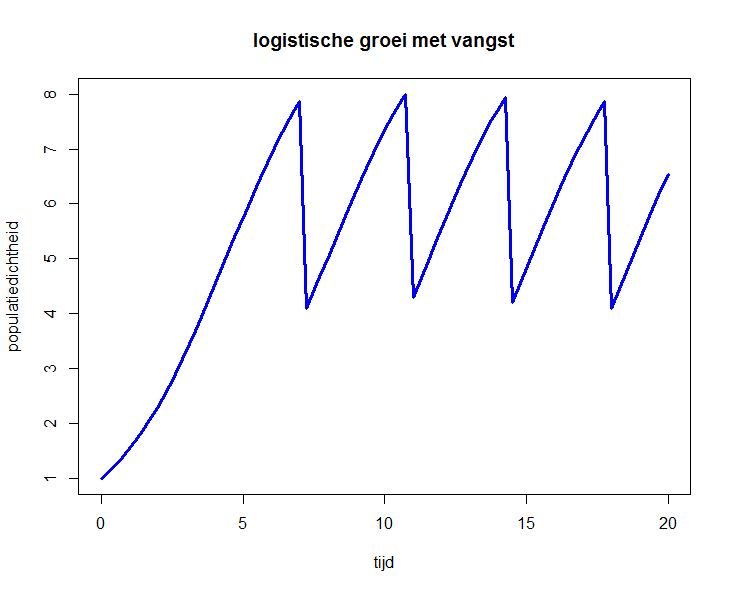
Populatiemodel met regulering We bekijken een populatiemodel van logistische groei gegeven door de volgende differentiaalvergelijking \[\frac{\dd y}{\dd t}=r\cdot y\cdot \left(1-\frac{y}{K}\right)\] voor zekere waarden van de relatieve groeisnelheidsconstante \(r\) en de draagkracht \(K\). Maar wanneer de populatiedichtheid \(y\) \(80\%\) van de maximale omvang bereikt heeft, wordt deze door vangst abrupt gehalveerd, om daarna weer ongemoeid te laten tot deze gebeurtenis zich herhaald. Deze vorm van regulering op basis van gebeurtenissen kun je ook in wiskundige software simuleren.
Implementatie van regulering in R Voor het gemak kiezen we \(r=0.5\), \(K=10\) en \(y(0)=1\), maar de implementatie van het populatiemodel is algemeen geformuleerd zodat je gemakkelijk andere waarden kan kiezen. De vangst wordt aangewakkerd doordat een bepaalde conditie bereikt wordt: in dit geval als de populatiedichtheid \(y\) gelijk wordt aan \(0.8K\). De aanwakkering van de gebeurtenis ("triggering") regel je in het deSolve pakket via rootfunc, een functie die moet signaleren dat \(y-0.8K\) de waarde \(0\) bereikt. De afhandeling van de gebeurtenis, dat wil zeggen hetgeen er moet gebeuren bij aanwakkering van de gebeurtenis, regel je in de eventfunc functie: in dit geval halveren we dan de populatiedichtheid. In onderstaand R script zie je hoe dit gedaan kan worden. Het komt er op neer dat je de naam rootfunc en eventfunc als opties mee moet geven in het ode commando.
library(deSolve)
model <- function(tijd, begintoestand, parameters){
with(as.list(c(begintoestand, parameters)), {
dydt <- r * y * (1 - y / K)
list(dydt)
})
}
rootfunc <- function(t, y, parameters) {
with(as.list(c(parameters)), {
return(y - 0.8 * K)
})
}
eventfunc <- function(t, y, parameters) {
y <- y/2
return(y)
}
y0 <- c(y=1)
params <- c(r=0.5, K=10)
t <- seq(from=0, to=20, by=0.25)
oplossing <- ode(y0, t, model, params,
rootfun = rootfunc,
events = list(func = eventfunc,
root = TRUE)
)
plot(oplossing, col="blue", lwd = 3,
main = "logistische groei met vangst",
xlab = "tijd", ylab="populatiedichtheid")Bovenstaand R script levert het volgende diagram op:
