Werken met R bij wiskunde: Differentiaalvergelijkingen in R
Stabiliteitsonderzoek bij een autonome, eerste-orde differentiaalvergelijking
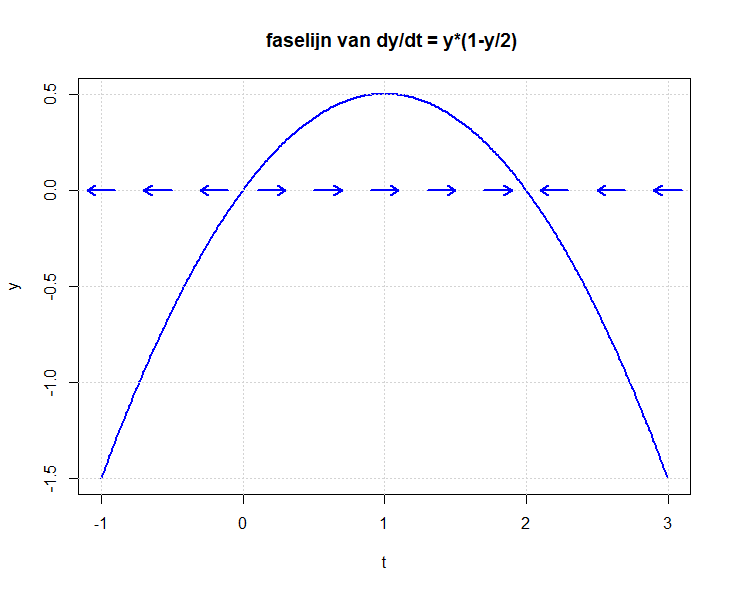
Het phaseR pakket heeft de commando's stability en phasePortrait om bij een autonome, eerste-orde differentiaalvergelijking de stabiliteit van evenwicht te bepalen en een faseportret te construeren. Maar wat in dit pakket faseportret genoemd wordt, heet in de literatuur ook wel faselijn. We illustreren het gebruik van het phaseR pakket aan de hand van de differentiaalvergelijking \[\frac{\dd y}{\dd t}=y\cdot (1-y/2)\] Deze differentiaalvergelijking heeft een aantrekkend evenwicht \(y=2\) en een afstotend evenwicht \(y=0\). In onderstaand R script wordt dit bevestigd. Ook wordtde faselijn getekend. We verwijzen naar de phaseR handleiding voor meer details over de verschillende opties in de stability en phasePortrait commando's.
library(phaseR)
model <- function(t, begintoestand, parameters){
with(as.list(c(begintoestand, parameters)), {
dydt <- r*y*(1-y/K)
return(list(dydt))
})
}
params <- c(r = 1, K = 2)
cat("\nStabiliteit y = 0:\n")
stability(model, ystar = 0, parameters = params,
system = "one.dim", state.names = c("y"))
cat("\n\nStabiliteit y = 2:\n")
stability(model, ystar = 2, parameters = params,
system = "one.dim", state.names = c("y"))
phasePortrait(model, ylim = c(-1,3), ystep = 0.01,
parameters = params, state.names = c("y"),
points = 11, frac = 0.5, arrow.head = 0.1,
col = "blue", lwd = "2", xlab = "t", ylab = "y",
main = "faselijn van dy/dt = y*(1-y/2)",
add.grid = TRUE)In het console venster staat dan
Stabiliteit y = 0:
Discriminant: 1 Classification: Unstable
Stabiliteit y = 2:
Discriminant: -1 Classification: Stableen het volgende diagram wordt getekend:
