Het phaseR pakket heeft het flowField commando aan boord om het faseportret, ook wel richtingsveld genoemd, van een autonoom stelsel van twee differentiaalvergelijkingen te tekenen. We illustreren dit aan de hand van het volgende Lotka-Volterra systeem \[\left\{\begin{aligned} \frac{\dd x}{\dd t} &= x\cdot (a-b\cdot y) \\[0.25cm] \frac{\dd y}{\dd t} &=y\cdot(c\cdot x-d)\end{aligned} \right.\] met \[a=0.4,\quad b=0.3,\quad c=0.1,\quad d=0.2\] Onderstaand R script

library(phaseR)

model <- function(tijd, begintoestand, parameters){
  with(as.list(c(begintoestand, parameters)),{
    dxdt <- x * (a - b*y)  
    dydt <- y * (c*x - d)
    return(list(c(dxdt, dydt)))
  })
}

params <- c(a = 0.4, b = 0.3, c = 0.1, d = 0.2)

flowField(model, xlim = c(0, 5), ylim = c(0, 3), 
          parameters = params, system = "two.dim",
          state.names = c("x", "y"), points = 21, 
          add = FALSE, xlab ="x", ylab ="y", 
          main = "fasevlak analyse van Lotka-Volterra systeem")

nullclines(model, xlim = c(-0.01, 5), ylim = c(-0.01,3), 
           parameters = params, system = "two.dim", 
           state.names = c("x", "y"), 
           col=c("green","red"), lwd = 3, add = TRUE)

trajectory(model, y0 = c(1.5, 2), tlim = c(0, 25), 
           parameters = params, state.names = c("x", "y"), 
           lwd = 2)
trajectory(model, y0 = c(1, 2.25), tlim = c(0, 25), 
           parameters = params, state.names = c("x", "y"), 
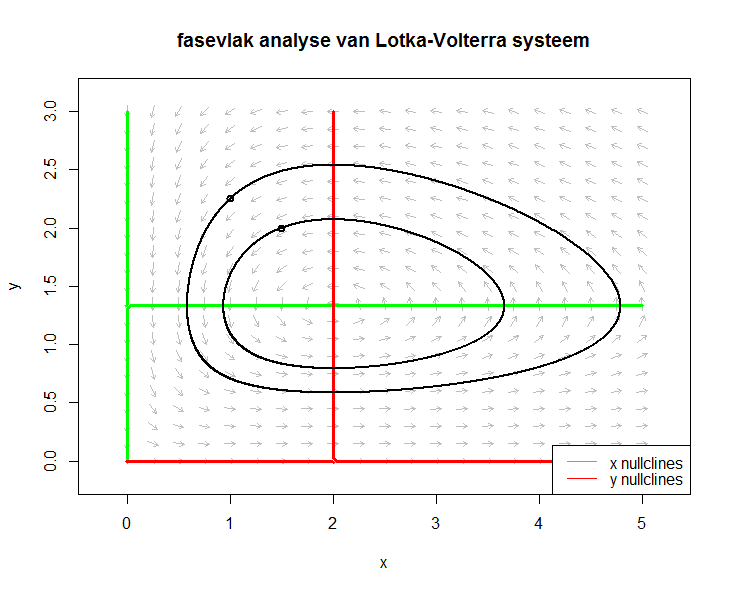
           lwd = 2)

tekent een richtingsveld voor het stelsel met daarin opgenomen de \(x\)- en \(y\)-nul-isoclienen en twee oplossingskrommen, die een gesloten baan vormen vanwege periodieke oplossingen.

Andere voorbeelden zijn in het phaseR pakket opgenomen en worden beschreven op https://cran.r-project.org/web/packages/phaseR/vignettes/introduction.html Zo kun je hierin lezen dat het phasePlaneAnalysis commando een analyse in het fasevlak te doen zonder dat je afzonderlijk functies hoeft te gebruiken. In ons voorbeeld zou je alleen het volgende R script hoeven te gebruiken en dan de gewenste opties te kiezen:

phasePlaneAnalysis(model, xlim = c(0, 5), ylim = c(0, 3), 
          parameters = params, system = "two.dim",
          state.names = c("x", "y"))