Basic skills in R: Working with data structures
Matrix
Explanation
A matrix (plural matrices) is a rectangular scheme with rows and colomns that are filled with values of the same data type. It is by definition a 2-dimensional object and the smallest components of a matrix are commonly called matrixelements or elements. Most matrices are numerical, i.e. they are filled with numbers, but it is possible to create matrices of other data types as well, such as character matrices. On the right-hand side you are examples of numerical and character matrices. The numerical matrix is written in the usual notation, in which the rectangular scheme is surrounded by parentheses.
Examples
A numerical matrix: \[\matrix{7 & 5 & 2\\ 4 & 1 & 4\\ 8 & 0 & 5}\] A character matrix with book genres:
| Thriller | Fantasy | Fantasy |
| Thriller | Detective | Thriller |
| Science fiction | Fantasy | Science fiction |
Explanation
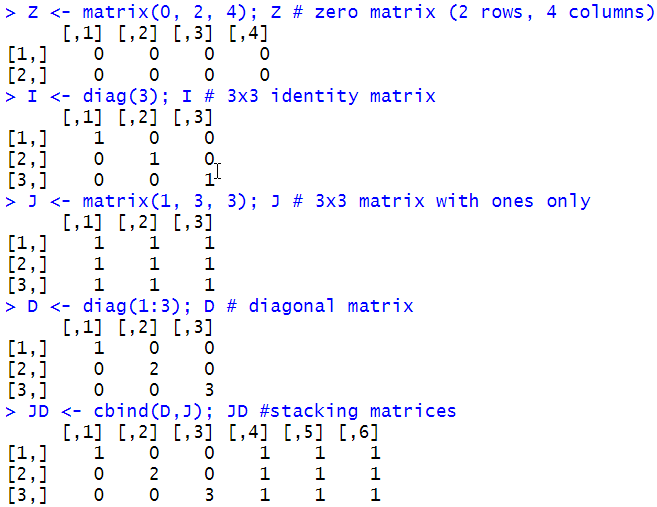
You can create a matrix with the function matrix(). The first argument of this function is a vector of values, the second argument is the number of rows and the third one is the number of columns. The fourth argument is logical and it specifies whether the matrix is to be populated by row (byrow = TRUE) or by column (byrow = FALSE, the default choice). You can also use named arguments and then the order of the named arguments does not matter.
You can display as well as specify the dimension of a matrix via the function dim().
Like vectors, matrices are subscriptable and mutable objects.
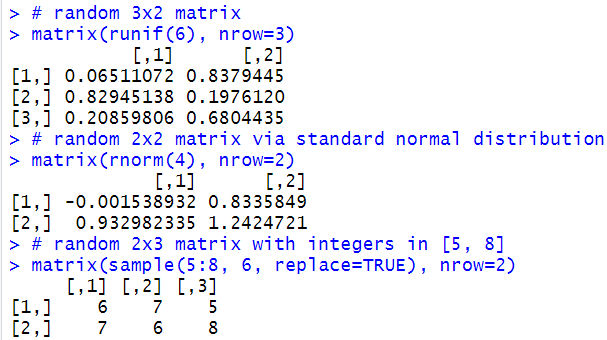
In simulations one make extensive use of matrices with random numbers, i.e., with randomly generated numbers. They make use of the following functions for generating random vectors:
runif() |
random numbers between 0 and 1 using a uniform distribution |
sample() |
objects randomly taken from a vector |
rnorm() |
random numbers using a normal distribution |
See the sample session on the right-hand side and practise with the creation of matrices.
Sample session
Explanation
There are special ways to create matrices and vectors with ones and zeros and to create diagonal matrices and identity matrices (via the function diag()). You can also stack matrices horizontally (cbind()) and vertically (rbind()). See the sample sesison on the right-hand side
Sample session
Arithmetic with matrices
Explanation
A matrix can be multiplied by a scalar or one could add a scalar to it: this is done elementwise. Matrices can be added to and multiplied with each other or with vectors if the dimensions of the objects involved allow it. The sample session on the right-hand side illustrates this.
The examples also show that matrix multiplication in the linear algebra sense is done via the operator %*%.
R provides numerous functions for matrix manipulation, such as calculating determinants, inverses, eigenvalues and eigenvectors, SVD, and so on. For further matrix algebra we refer to the linear algebra in R chapter of the SMASH course Doing Mathematics with R.
Sample session
Selecting elements of matrices and assigning values
Explanation
Like vectors, matrices are subscriptable and mutable objects. This means that elements of a matrix can be accessed via a positional index and that you can change a matrix also by assigning a value to a single element. The positonal index consists of the row and column index.
Indexing allows for selecton of submatrices. Selection of row or columns based on a condition is possible as well.
Take a close look at the examples in the sample session on the right-hand side and experiment a bit with it to gain experience in submatrix selection.
Sample session
We consider the following matrices \[A=\left(\begin{array}{rrr} -3 & -1 & 0 \\ 4 & 7 & -10 \\ 4 & 3 & -3 \end{array}\right), \quad B=\left(\begin{array}{rrr} -2 & 2 & -5 \\ 12 & -7 & 20 \\ 6 & -4 & 11 \end{array}\right), \quad C=\left(\begin{array}{rrr} -2 & 14 & 8 \\ -1 & 10 & 6 \\ 1 & -13 & -8 \end{array}\right)\] These matrices have the following properties: \[A^{4n+1}=A,\quad B^n=B,\quad C^{n+2}=0,\] for \(n=1,2\ldots\). Verify these propertiesn in R.
