Gamma function and factorial The gamma function \(\Gamma(x)\) is defined for all real \(x\) except zero and negative integers by \[\Gamma(x)=\int_0^{\infty}t^{x-1}e^{-t}\,\dd t\] The factorial function is defined by \[x!=\Gamma(x+1)\] For a natural number \(n\) we have \[n! = 1\times 2 \times\cdots\times (n-1)\times n\] In R, we can use the functions gamma() and factorial() to compute values of the gamma function and the factorial function, respectively.

> factorial(4)
[1] 24
> gamma(5)
[1] 24
> gamma(1/2) - sqrt(pi)  # in exact arithmetic equal to 0
[1] 2.220446e-16

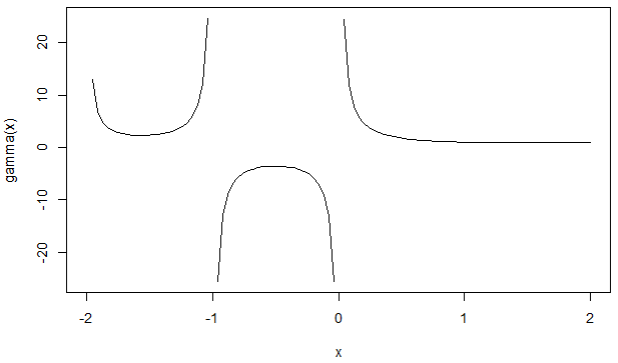
> curve(gamma, -2,2)
Warning message:
In gamma(x) : NaNs produced

Binomial coefficient For natural numbers \(n\) and \(0\le k\le n\), the binomial coefficient \(\binom{n}{k}\) is defined as \[\binom{n}{k}= \frac{n!}{k!\times(n-k)!}\] For example, \[\binom{5}{2}= \frac{5!}{2!\cdot 3!} =10 \] In R, the function choose() can be used for computing a binomial coefficient.

> choose(5,2)
[1] 10

Combinations and permutations When we have \(n\) distinct objects, then we can order them in a sequence in \(n!\) ways. Each ordering is called a permutation of the object. In R, you can randomly generate a permutation with the function sample().

> set.seed(123)
> sample(3)  # a random permuation of 1, 2, 3
[1] 3 1 2
> sample(3)  # a random permuation of 1, 2, 3
[1] 2 1 3
> sample(3)  # a random permuation of 1, 2, 3
[1] 2 3 1

> sample(c("a", "b", "c")) # a random permutation of "a", "b", "c"
[1] "a" "b" "c"
> sample(c("a", "b", "c")) # a random permutation of "a", "b", "c"
[1] "b" "a" "c"
> sample(c("a", "b", "c")) # a random permutation of "a", "b", "c"
[1] "c" "b" "a"

In \(\binom{n}{k}\) ways you can select \(k\) objects from a set of \(n\) distinct objects, without taking concern of the order in which you selected objects. Fine, but can you generate in R such \(\boldsymbol{k}\)-combinations from a set of \(n\) distinct objects? The answer is yes, namely via the package combinat. The session below shows examples.

> install.packages("combinat")
> library(combinat)
> permn(1:3)  # generate all 6 permutations of 1, 2, 3
[[1]]
[1] 1 2 3

[[2]]
[1] 1 3 2

[[3]]
[1] 3 1 2

[[4]]
[1] 3 2 1

[[5]]
[1] 2 3 1

[[6]]
[1] 2 1 3
> permn(c("a","b"))  # generate all permutations of "a", "b"
[[1]]
[1] "a" "b"

[[2]]
[1] "b" "a"
> combn(1:3,1)           # selections of 1 number from {1, 2, 3}
     [,1] [,2] [,3]
[1,]    1    2    3
> combn(1:3,2)           # selections of 2 numbers from {1, 2, 3}
     [,1] [,2] [,3]
[1,]    1    1    2
[2,]    2    3    3
> combn(1:3,3)           # selection of 3 numbers from {1, 2, 3}
[1] 1 2 3
> combn(letters[1:4], 2) # selections of 2 letters from {"a", "b", "c", "d"}
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,] "a"  "a"  "a"  "b"  "b"  "c" 
[2,] "b"  "c"  "d"  "c"  "d"  "d" 
> combn(letters[1:4], 2, simplify = FALSE)  # idem
[[1]]
[1] "a" "b"

[[2]]
[1] "a" "c"

[[3]]
[1] "a" "d"

[[4]]
[1] "b" "c"

[[5]]
[1] "b" "d"

[[6]]
[1] "c" "d" 

Alternatively you could have used the package gtools. This package is more flexible as it allows to calculate the permutations and combinations both without and with repetition.