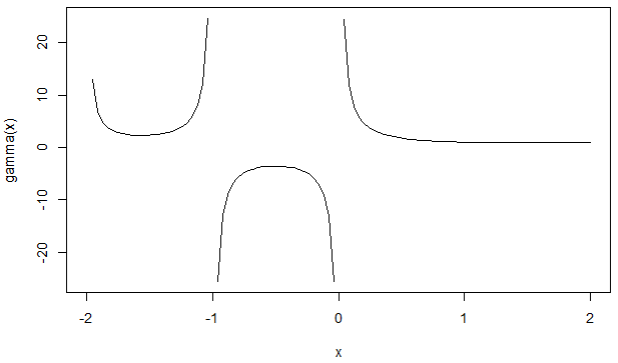
Gammafunctie en faculteit De gammafunctie \(\Gamma(x)\) is voor alle reële getallen \(x\) behalve nul en negatieve gehele getallen door \[\Gamma(x)=\int_0^{\infty}t^{x-1}e^{-t}\,\dd t\] The faculteit is gedefinieerd door \[x!=\Gamma(x+1)\] Voor een natuurlijk getal \(n\) hebben we \[n! = 1\times 2 \times\cdots\times (n-1)\times n\] In R kun je de functies gamma() en factorial() gebruiken om waarden uit te rekenen von respectievelijk de gammafunctie en de faculteit

> factorial(4)
[1] 24
> gamma(5)
[1] 24
> gamma(1/2) - sqrt(pi)  # in exact rekenen gelijk aan 0
[1] 2.220446e-16

> curve(gamma, -2,2)
Warning message:
In gamma(x) : NaNs produced

Binomialcoëfficiënt Voor natuurlijke getallen \(n\) en \(0\le k\le n\) wordt de binomiaalcoëfficënt \(\binom{n}{k}\) gedefinieerd door \[\binom{n}{k}= \frac{n!}{k!\times(n-k)!}\] Bijvoorbeeld \[\binom{5}{2}= \frac{5!}{2!\cdot 3!} =10 \] In R kun je de functie choose() gebruiken om een binomiaalcoëfficiënt uit te rekenen.

> choose(5,2)
[1] 10

Combinatie en permutaties Wanneer we \(n\) verschillende objecten hebben, kunnen we ze op \(n!\) manieren rangschikken. Elke rangschikking heet een permutatie van de \(n\)-verzameling object. In R kun je een willekeurige permutatie genereren met de functie sample().

> set.seed(123)
> sample(3)  # een willekeurige permutatie van 1, 2, 3
[1] 3 1 2
> sample(3)  # een willekeurige permutatie van 1, 2, 3
[1] 2 1 3
> sample(3)  # een willekeurige permutatie van 1, 2, 3
[1] 2 3 1

> sample(c("a", "b", "c")) # # een willekeurige permutatie van "a", "b", "c"
[1] "a" "b" "c"
> sample(c("a", "b", "c")) # # een willekeurige permutatie van "a", "b", "c"
[1] "b" "a" "c"
> sample(c("a", "b", "c")) # # een willekeurige permutatie van "a", "b", "c"
[1] "c" "b" "a"

Op \(\binom{n}{k}\) manieren kun je \(k\) objecten uit een verzameling met \(n\) verschillende objecten selecteren zonder rekening te houden met de volgorde van selectie. Mooi, maar kun je in R dergelijke \(\boldsymbol{k}\)-combinaties uit een verzameling van\(n\) verschillende objecten maken? Het antwoord op deze vraag is ja, namelijk m.b.v. het pakket combinat. Hieronder zijn enkele voorbeelden.

> install.packages("combinat")
> library(combinat)
> permn(1:3)  # genereer alle 6 permutaties van 1, 2, 3
[[1]]
[1] 1 2 3

[[2]]
[1] 1 3 2

[[3]]
[1] 3 1 2

[[4]]
[1] 3 2 1

[[5]]
[1] 2 3 1

[[6]]
[1] 2 1 3
> permn(c("a","b"))  # genereer alle permutaties van "a", "b"
[[1]]
[1] "a" "b"

[[2]]
[1] "b" "a"
> combn(1:3,1)           # selecties van 1 getal uit {1, 2, 3}
     [,1] [,2] [,3]
[1,]    1    2    3
> combn(1:3,2)           # selecties van 2 getallen uit {1, 2, 3}
     [,1] [,2] [,3]
[1,]    1    1    2
[2,]    2    3    3
> combn(1:3,3)           # selectie van 3 getallen uit {1, 2, 3}
[1] 1 2 3
> combn(letters[1:4], 2) # selecties van 2 letters uit {"a", "b", "c", "d"}
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,] "a"  "a"  "a"  "b"  "b"  "c" 
[2,] "b"  "c"  "d"  "c"  "d"  "d" 
> combn(letters[1:4], 2, simplify = FALSE)  # idem
[[1]]
[1] "a" "b"

[[2]]
[1] "a" "c"

[[3]]
[1] "a" "d"

[[4]]
[1] "b" "c"

[[5]]
[1] "b" "d"

[[6]]
[1] "c" "d" 

Als alternatief had je het pakket gtools kunnen gebruiken. Dit pakket is flexibeler omdat het mogelijk maakt zowel permutaties als combinaties te berekenen, met en zonder herhaling.