Basisvaardigheden in R: Grafieken: de basis
 Q-Q diagram (kwantiel-kwantiel diagram)
Q-Q diagram (kwantiel-kwantiel diagram)
Een Q-Q diagram, minder bekend als kwantiel-kwantiel diagram, is een spreidingsdiagram dat wordt gebruikt om de normaliteit van een bepaalde dataset visueel te controleren. Bij bijna-normaliteit liggen de punten in het Q-Q diagram dicht bij een rechte lijn. Eigenlijk hebben deze punten de experimentele kwantielen en de theoretische kwantielen (z-waarden) voor de normale verdeling als coördinaten.
Voorbeeld van een bijna normaal verdeelde steekproef
R-script
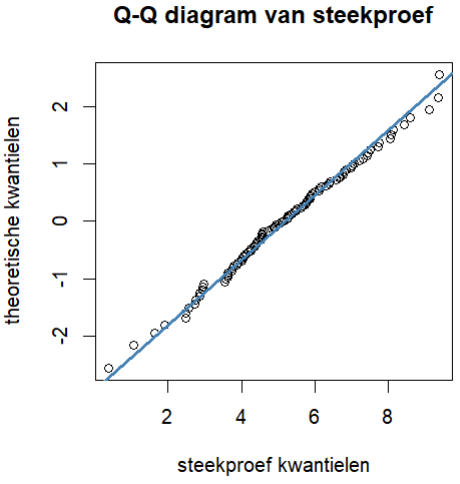
In het eerste voorbeeld creëren we een steekproef van willekeurige getallen voor de normale verdeling met gemiddelde waarde 5 en standaarddeviatie 2. Met de functie qqnorm() creëren we een Q-Q diagram van de steekproefwaarden; de optie datax = TRUE wordt gebruikt om de steekproef kwantielen op de x-as te laten staan. Met qqline() voegen we een referentielijn toe.
set.seed(123)
x <- rnorm(n = 100, mean = 5, sd = 2)
qqnorm(x, datax = TRUE,
xlab = "steekproef kwantielen",
ylab = "theoretische kwantielen",
main = "Q-Q diagram van steekproef") qqline(x, data = TRUE, col = "steelblue", lwd = 3)
Q-Q diagram
Voorbeeld met de ToothGrowth-dataset
R heeft een ingebouwde dataset ToothGrowth die de lengte bevat van odontoblasten (cellen die verantwoordelijk zijn voor tandgroei) bij 60 cavia's die deel uitmaken van een klinische studie. We controleren visueel de normaliteit van de lengtegegevens via het volgende script.
lengte <- ToothGrowth$len
qqnorm(lengte, frame = FALSE,
xlab = "theoretische kwantielen",
ylab = "steekproef kwantielen",
main = "Q-Q diagram van steekproef")
qqline(lengte, col = "steelblue", lwd = 3)
Het diagram aan de rechterkant laat zien dat de normaliteit van de dataset minder goed is bij de extreme steekpoef kwantielen.
Q-Q diagram

Q-Q diagram voor elke distributie Met de functie qqplot() kunt u voor elke verdeling een Q-Q maken maken. In tegenstelling tot de functie qqnorm() moet je twee argumenten opgeven: de eerste set gegevens en de tweede set kwantielen voor de distributie.
Uitleg en R-script
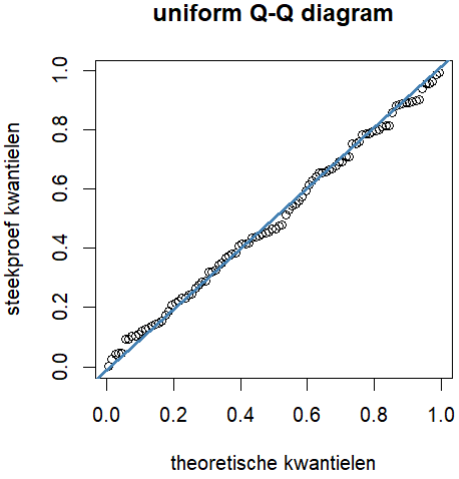
In ons R-script hieronder genereren we eerst willekeurige waarden tussen \(0\) en \(1\) voor de uniforme verdeling. Een normaal Q-Q diagram van de steekproef laat zien dat de gegevens niet normaal verdeeld zijn. De functie ppoints() genereert een bepaald aantal kansen of verhoudingen. De functie qunif() toegepast op een reeks verhoudingen retourneert vervolgens hetzelfde aantal kwantielen uit een uniforme verdeling voor de gegeven verhoudingen. In een Q-Q diagram voor de uniforme verdeling zien we dat de punten dicht bij de referentielijn liggen en dat de gegenereerde dataset dus uniform verdeeld is.
set.seed(123)
n <- 100
y <- runif(n = n, min = 0, max = 1) # sample
x <- qunif(ppoints(n)) # theoretische kwantielen
qqnorm(y, main="normaal Q-Q diagram",
xlab = "theoretische kwantielen",
ylab = "steekproef kwantielen"
)
qqline(y, col = "steelblue", lwd = 3)
qqplot(x,y, main="uniform Q-Q diagram",
xlab = "theoretische kwantielen",
ylab = "steekproef kwantielen"
)
qqline(y, distribution = qunif,
col = "steelblue", lwd = 3)
Q-Q diagrams