Voorbeeld van humane lichaamsgroei We gebruiken gegevens over de groei van Nederlandse kinderen van Marokkaanse afkomst, gemeten voor leeftijden tussen 1 en 18 jaar. De gegevens zijn afkomstig van de Nederlandse Groeistudie uit 2010. We willen de twee groeikrommen in één grafiek weergeven met verschillende kleuren en symbolen voor de datapunten, en we willen een legenda toevoegen die de twee grafieken identificeert.

Eerst voeren we de gegevens in.

> leeftijd <- 1:18
> lengte_jongens <- c(76.1, 87.7, 96.8, 104.5, 111.4, 117.7, 123.9, 129.4, 134.6,
+                     140.1, 145.4, 150.5, 156.3, 163.3, 169.9, 174.0, 176.1, 177.2)
> lengte_meisjes <- c(75.0, 86.5, 96.0, 103.5, 110.2, 116.8, 123.0, 128.4, 134.1,
+                      140.2, 147.0, 152.9, 157.3, 160.4, 162.4, 162.8, 162.8, 162.8)

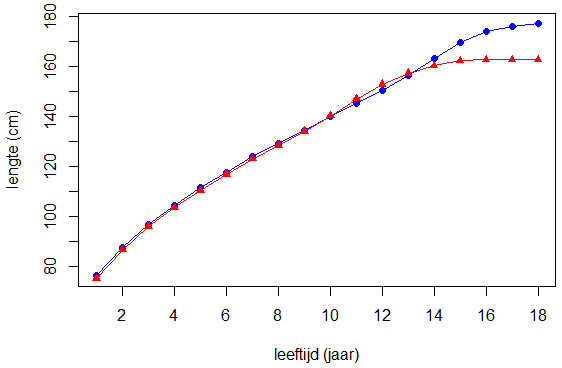
Vervolgens plotten we de gemiddelde lengte (in cm) van jongens van Marokkaanse afkomst tegen hun leeftijd in de blauwe kleur en gebruiken we een gesloten cirkel als symbool voor de datapunten. Het type van de grafiek is zodanig dat er een overlay van lijnen en punten is.

> plot(x = leeftijd, y = lengte_jongens, xlab = "leeftijd (jaar)", ylab = "lengte (cm)", 
+      type = "o", col = "blue", pch = 16)

Een grafiek zal verschijnen in een grafiekvenster. Via de laag-niveau plotfunctie points() kunnen we de groeikromme van meisjes van Marokkaanse afkomst toevoegen aan het grafiekvenster; hier kiezen we voor de rode kleur en een gesloten driehoek als symbool voor een datapunt. We tekenen geen nieuwe labels op de assen.

> points(x = leeftijd, y = lengte_meisjes, xlab = "", ylab = "", 
+        type = "o", col = "red", pch = 17)

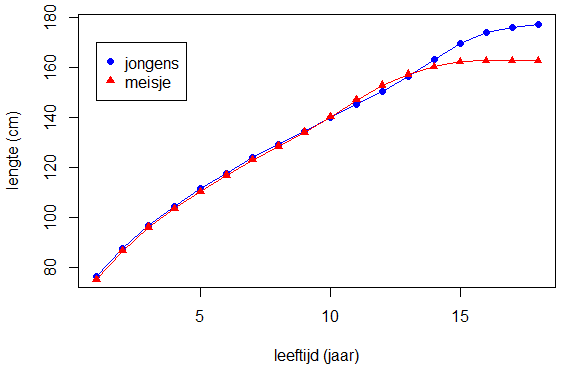
Met de functie legend() kunnen we een legenda toevoegen op een gespecificeerde locatie die de gebruikte kleuren en symbolen uitlegt.

> legend(1, 170, legend = c("jongens", "meisje"), col = c("blue", "red"), pch = c(16,17))

Dit levert het volgende diagram op:

De locatie van de legenda kan ook worden gespecificeerd door een enkel trefwoord uit de lijst. "bottomright", "bottom", "bottomleft", "left", "topleft", "top", "topright", "right", en "center".

In plaats van de laag-niveau plotfunctie points(), hadden we ook de laag-niveau plotfunctie lines() kunnen gebruiken.

Statistisch voorbeeld In dit voorbeeld genereren we 200 willekeurige getallen uit de standaardnormale verdeling en tekenen we een histogram met relatieve frequentie met een bakgrootte die impliciet is gebaseerd op het bereik van de gegevens. Ter vergelijking voegen we de grafiek van de dichtheidsfunctie van de standaardnormale verdeling toe aan de grafiek..

Allereerst gebruiken we de functie rnorm() om een lijst van willekeurige getallen te genereren volgens de standaardnormale verdeling.

> set.seed(123)   # stel seed in voor reproduceerbaarheid
> x <- rnorm(200) # genereer willekeurige getallen

Vervolgens construeren we het histogram van de reeks willekeurige getallen, maar maken we nog geen grafiek omdat we eerst de verticale bereik van onze beoogde grafiek willen berekenen om ervoor te zorgen dat alles zichtbaar zal zijn.

> h <- hist(x, plot=FALSE)               # genereer een histogram zonder te tekenen
> y_range <- range(0, h$density, dnorm(0))  # bepaal min en max van verticaal bereik

We zijn klaar om het beoogde histogram te plotten. Het argument freq = FALSE in de functie hist() zorgt ervoor dat het histogram wordt weergegeven in termen van dichtheden in plaats van absolute tellingen. We kleuren de staven geel.

> hist(x, freq = FALSE, ylim = y_range, col = "yellow")

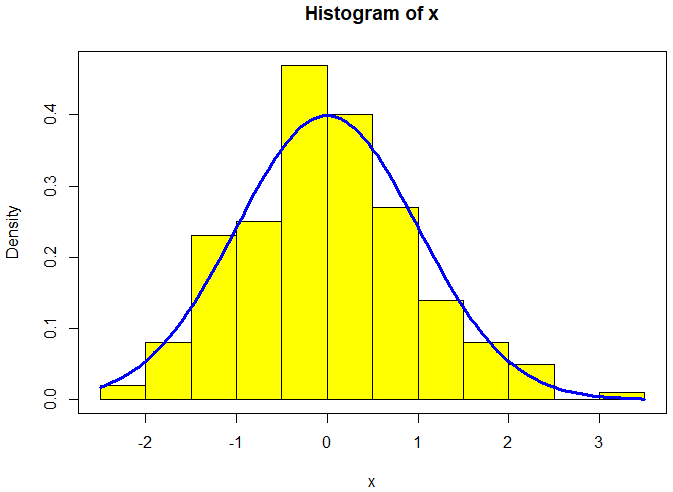
We gebruiken de functie curve() om de grafiek van de dichtheidsfunctie van de normale verdeling toe te voegen als een dikke blauwe curve en omkaderen de grafiek

> curve(dnorm(x), add = TRUE, col = "blue", lwd = 3)
> box()

Het onderstaande diagram is op deze manier gecreëerd:

Punten en lijnen combineren We geven een voorbeeld waarin we punten genereren op een rechte lijn, maar vervolgens wat ruis toevoegen. We plotten de datapunten en tekenen de rechte lijn die we hebben gebruikt om de punten te genereren.

In R kunnen we ruis simuleren met de functie jitter().

Allereerst creëren we de coördinaten van punten op de lijn \(y = 1 + 3x \) zonder enige ruis.

> x_waarden <- seq(from = 0, to = 10, by = 0.2)
> y_waarden <- 1 + 3*x_waarden

Nu gaan we de ruis definiëren. We passen het argument amount in de functie jitter(), omdat dit ons in staat stelt de reikwijdte van de ruis nauwkeurig te regelen. We kiezen voor een meetfoutmarge van 2 aan de onderkant en 2 aan de bovenkant.

We simuleren alleen ruis over de \(y\)-waarden, omdat dit de responsvariabele is die gemeten wordt. Dit is dus ook de variabele waarin in de praktijk meetfouten zullen voorkomen waarvoor je moet corrigeren.

Met de functie set.seed() zorgen we ervoor dat de willekeurige getallengenerator in R elke keer dezelfde reeks willekeurig getrokken getallen genereert. Dit zorgt voor reproduceerbare simulaties. Het natuurlijke getal 123 dat in de code wordt gebruikt, kan worden gekozen als startpunt voor een simulatie.

> set.seed(123)
> y_waarden_met_ruis <- jitter(x = y_waarden, amount = 2)

We plot the data points and use the low-level plotting function abline() to add a straight line \(y=a+ b\,x\) to the diagram; we only have to specify the values of the \(y\)-intercept and the slope of the line.

> plot(x = x_waarden, y = y_waarden_met_ruis, xlab = "x", ylab = "y",
+      type = "p", pch = 20, col = "Maroon4", 
+      main = "ruis in datapunten m.b.t. de lijn y = 1 + 3x")
> abline(a = 1, b = 3, col = "Orange2", lwd = 3)  # voeg de lijn toe

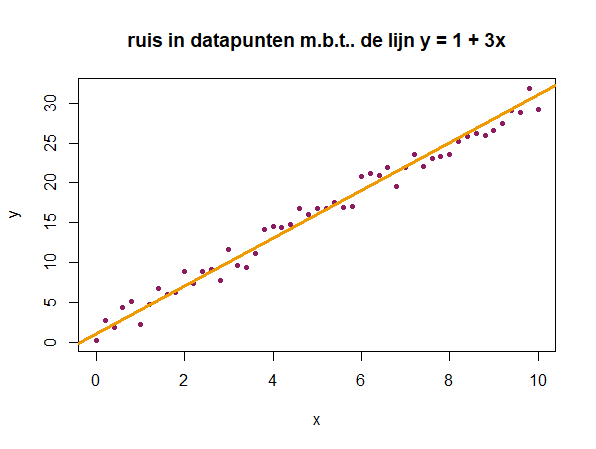
Combining graphs of functions

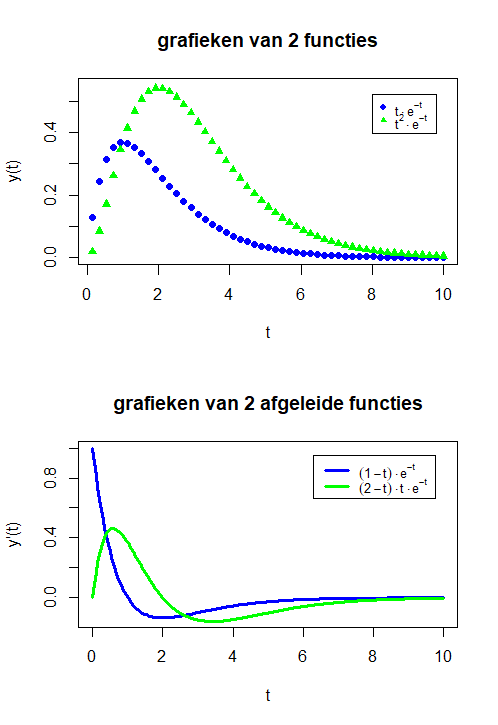
We kunnen grafieken onder of naast elkaar zetten om ze met elkaar te vergelijken. In het volgende R script worden de grafieken van de functies \[f_1(t)=te^{-t},\quad f_2(t)=t^2e^{-t}\] in één diagram getekend met daaronder de grafieken van hun eerste afgeleiden \[f_1'(t)=(1-t)te^{-t},\quad f_2'(t)=(2-t)te^{-t}\] in een ander diagram getekend. Samen vormen ze één figuur. De functie die een figuur in meerdere delen opsplitst is de volgende functie: par(mfrow=c(2,1)) vult \(2\) rijen en \(1\) kolom met diagrammen. We hebben dit keer de formules in de legenda meer in wiskundige notatie gezet via de expression functie.

# definieer de functies en hun afgeleiden
f1  <- function(t) { t * exp(-t) }
f2  <- function(t) { t^2 * exp(-t) }
f1p <- function(t) { (1-t) * exp(-t) }
f2p <- function(t) { (2-t) * t * exp(-t) }

# maak tijdsintervallen en functiewaarden
t   <- seq(from=0, to=10, length=204)
tt  <- t[seq(0,204, by=4)]
y1  <- f1(tt)
y2  <- f2(tt)
y1p <- f1p(t)
y2p <- f2p(t)

par(mfrow=c(2,1)) # 2 diagrammen onder elkaar

# bovenste diagram met grafieken van functies
plot(tt, y1, type="p", col="blue", pch=16, lwd=3, ylim=c(0,0.55),
  main="grafieken van 2 functies", xlab="t", ylab="y(t)")
points(tt, y2, type="p", col="green", pch=17, lwd=3)
legend(8, 0.52, text.width=1, 
  legend=expression(t%.%e^-t,t^2%.%e^-t),
  col=c("blue", "green"), pch=c(16,17), cex=0.8)
# onderste diagram met grafieken van afgeleiden
plot(t, y1p, type="l", col="blue", lwd=3, ylim=c(-0.15,1),
  main="grafieken van 2 afgeleide functies", 
  xlab="t", ylab="y'(t)")
lines(t, y2p, type="l", col="green", lwd=3)
legend(6.3, 0.95, text.width=2,
  legend=expression((1-t)%.%e^-t, (2-t)%.%t%.%e^-t), 
  col=c("blue", "green"), lwd=3, cex=0.8)

Het resultaat ziet er als volgt uit: