Doorsnede

De doorsnede van twee verzamelingen \(A\) en \(B\), genoteerd als \(A\cap B\), is de verzameling van alle elementen die behoren tot \(A\) en tot \(B\). In formulevorm: \[A\cap B=\{x \mid x\in A\text{ en } x\in B\}\] We noemen twee verzamelingen \(A\) en \(B\) disjunct als \(A\cap B=\emptyset\).

Analoog de doorsnede van geïndexeerde verzamelingen \(X_i\): \[\begin{aligned}\underset{i=1}{\overset{n}{\cap}}X_i&=X_1\cap X_2\cap X_3\cap \cdots\cap X_n\\ \underset{i=1}{\overset{\infty}{\cap}}X_i&=X_1\cap X_2\cap X_3\cap \cdots\end{aligned} \]

Voorbeelden

\[\{1,2,3\}\cap \{2,3,4\}=\{2,3\}\] \[[0,\infty)\cap (-1, 1)=[0,1)\] \[\{1,2\}\cap \{3,4\}=\emptyset\] \[\{1,2\}\cap \emptyset=\emptyset\]
Als \(X_i=\{x\mid x\in\mathbb{Z}^{+}\text{ en }x\ge i\}\), dan \[\begin{aligned}\underset{i=1}{\overset{n}{\cap}}X_i&= \{x\mid x\in\mathbb{Z}^{+}\text{ en }x\ge n\}\\ \underset{i=1}{\overset{\infty}{\cap}}X_i&=\emptyset\end{aligned} \]

Vereniging

De vereniging van twee verzamelingen \(A\) en \(B\), genoteerd als \(A\cup B\), is de verzameling van alle elementen die behoren tot \(A\) of tot \(B\). In formulevorm: \[A\cup B=\{x \mid x\in A\text{ of } x\in B\}\]

Analoog de vereniging van geïndexeerde verzamelingen \(X_i\): \[\begin{aligned}\underset{i=1}{\overset{n}{\cup}}X_i&=X_1\cup X_2\cup X_3\cup \cdots\cup X_n\\ \underset{i=1}{\overset{\infty}{\cup}}X_i&=X_1\cup X_2\cup X_3\cup \cdots\end{aligned} \]

Voorbeelden

\[\{1,2,3\}\cup \{2,3,4\}=\{1,2,3,4\}\] \[[0,\infty)\cap (-1, 1)=(-1,\infty)\] \[\{1,2\}\cup \{2\}=\{1,2\}\] \[\{1,2\}\cup \emptyset=\{1,2\}\]
Als \(X_i=\{x\mid x\in\mathbb{R}\text{ en }0\lt x\le i\}\), dan \[\begin{aligned}\underset{i=1}{\overset{n}{\cup}}X_i&= \{x\mid x\in\mathbb{R}\text{ en }0\lt x\le n\}\\ \underset{i=1}{\overset{\infty}{\cup}}X_i&=\mathbb{R}^{+}\end{aligned} \]

Verschil en complement

Als \(A\) en \(B\) verzamelingen zijn, dan is het verschil van A en B, genoteerd als \(A\backslash B\), de verzameling van alle elementen die behoren tot \(A\) en niet tot \(B\). In formulevorm: \[A\backslash B=\{x \mid x\in A\text{ en } x\notin B\}\] Als \(A\) het universum \(U\) is waarbinnen elementen van \(B\) gekozen zijn, dan noemen we \(U\backslash B\) het complement van \(B\) en noteren we dit als \(B^c\).

Uit de definitie van verschil volgt onmiddellijk dat voor elke verzameling \(A\) en het universum \(U\): \[\begin{aligned}A\backslash \emptyset &=A\\ A\backslash A &=\emptyset \\ \emptyset^{c}&=U\\ U^c&=\emptyset\end{aligned}\].

Voorbeelden

\[\{1,2,3\}\backslash\{1,3,5\}=\{2\}\] \[[0,\infty)\backslash (-1, 1)=[1,\infty)\] \[\{1,2\}\backslash\{3,4\}=\{1,2\}\] Als \(U=\mathbb{Z}\), dan \[\{0\}^c=\{n\in \mathbb{Z}\mid n\neq 0\}\] Als \(U=\mathbb{R}\), dan \[\begin{aligned}(-1,1){}^{c} &=(-\infty,-1]\cup[1,\infty)\\ &=\{x \mid x\le -1\text{ of } x\ge 1\}\end{aligned}\]

Symmetrisch verschil

Het symmetrisch verschil van twee verzamelingen \(A\) en \(B\), genoteerd als \(A\triangle B\), is in formulevorm: \[A\triangle B=(A\backslash B)\cup(B\backslash A)\text.\] Voor niet-disjuncte verzamelingen hoort hierbij onderstaand Venndiagram (zie later in deze sectie).

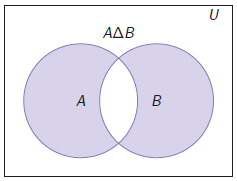
Dit Venndiagram illustreert ook: \[\begin{aligned} A\triangle B&=(A\cup B)\backslash (A\cap B)\\[0.25cm] A\triangle B&=B\triangle A\end{aligned}\]

Voorbeelden

\[\begin{aligned}\{1,2\}\triangle \{2,3,4\}&=\{1,3,4\}\\[0.25cm] \{a,b,c\}\triangle \{b,c,d\} &= \{a,d\}\end{aligned}\]
Voor een verzameling \(A\) geldt: \[A\triangle A=\emptyset\;\text{ en }\;A\triangle \emptyset=A\]