Naïeve verzamelingenleer: Relaties
 Basisbegrippen
Basisbegrippen
Het Cartesisch product \(X\times Y\) van verzamelingen \(X\) en \(Y\) is vooral geïntroduceerd om relaties te definiëren, waar functies weer een speciaal geval van zijn.
Relatie
Relatie
Een relatie \(R\) van een verzameling \(X\) naar \(Y\) is een deelverzameling \(R\subset X\times Y\) van \(X\times Y\). Als\((x,y)\) een element van de relatie \(R\) is, dan noteren we dit ook wel als \(xRy\). Als we willen benadrukken dat er twee verzamelingen betrokken zijn bij een relatie gebruiken we de naam binaire relatie.
Een relatie op \(X\) is een deelverzameling \(R \subset X\times X\).
Voorbeelden
Stel \(X=\{1,2\}\text{, }Y=\{2,3,4\}\) en \(R=\{(1,2), (1,3),(2,2)\}\). Dan is \(R\) een relatie van \(X\) naar \(Y\).
\(\{(x,y)\in \mathbb{R}\times\mathbb{R}\mid x<y\}\) is een relatie op \(\mathbb{R}\).
\(\{(x,y)\in \mathbb{N}\times\mathbb{N}\mid y=x+1\}\) is een relatie op \(\mathbb{N}\).
Als \(X\) een verzameling is, dan is \(\mathrm{Id}_X=\{(x,y)\in X^2\mid x=y\}\) een relatie, namelijk de identieke relatie op \(X\), ook wel genoemd de identiteit of diagonaal op \(X\).
Domein en bereik van een binaire relatie
Voor een binaire relatie \(R\) van een verzameling \(X\) naar \(Y\) definiëren we het domein \(\mathrm{dom}(R)\) en het bereik (range) \(\mathrm{ran}(R)\) als \[\begin{aligned} \mathrm{dom}(R)&=\{x\in X\mid\text{ er is een }y\in Y\text{ zodanig dat }xRy\}\\[0.25cm]\mathrm{ran}(R)&=\{y\in Y\mid\text{ er is een }x\in X\text{ zodanig dat }xRy\}\end{aligned}\]
Stel \(X=\{1,2\}\), \(Y=\{2,3,4\}\) en \(R=\{(1,2), (1,3),(2,2)\}\). Dan is \(R\) een relatie van \(X\) naar \(Y\) en \[\begin{aligned} \mathrm{dom}(R)&=\{1,2\}\\[0.25cm]\mathrm{ran}(R)&=\{2,3\}\end{aligned}\] Deze relatie kan als volgt grafisch worden weergegeven:
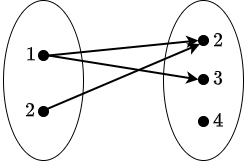
Inverse relatie
Inverse relatie
Voor een binaire relatie \(R\) van een verzameling \(X\) naar \(Y\) definiëren we de inverse relatie \(R^{-1}\) als de verzameling geordende paren \((y,x)\in Y\times X\) waarvoor \((x,y)\in R\).
Voorbeeld
Als \(R=\bigl\{(x,y)\in \mathbb{R}\times \mathbb{R}\mid x<y\bigr\}\) dan \(R=\bigl\{(x,y)\in \mathbb{R}\times \mathbb{R}\mid x>y\bigr\}\).
Samenstelling van relaties Voor een binaire relatie \(R\) van een verzameling \(X\) naar \(Y\) en een binaire relatie \(S\) van \(Y\) naar een verzameling \(Z\) definiëren we de samenstelling of compositie \(S\circ R\) van \(S\) en \(R\) als de verzameling geordende paren \((x,z)\in X\times Z\) waarvoor er een \(y\in Y\) is zodanig dat \((x,y)\in R\) en \((y,z)\in S\).
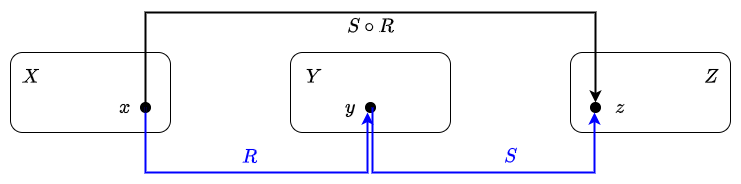
Stel dat \(R\) een relatie is van \(X\) naar \(Y\), \(S\) een relatie is van \(Y\) naar \(Z\) en dat \(T\) een relatie is van \(Z\) naar \(W\). Dan geldt:
- \((R^{-1})^{-1}=R\);
- \(\mathrm{dom}(R^{-1})=\mathrm{ran}(R)\);
- \(\mathrm{ran}(R^{-1})=\mathrm{dom}(R)\);
- \(T\circ(S\circ R)=(T\circ S)\circ R\);
- \((S\circ R)^{-1}=R^{-1}\circ S^{-1}\).


