Gelijkmachtigheid en (on)eindigheid

Naïeve verzamelingenleer: Grootte van een verzameling

Gelijkmachtigheid en (on)eindigheid

We noemen de verzameling \(X\) gelijkmachtig met de verzameling \(Y\), en zeggen ook wel dat \(X\) dezelfde cardinaliteit of hetzelfde aantal elementen als \(Y\) heeft, als er een bijectie \(f\:\;X\rightarrow Y\) bestaat. We noteren dit als \(X\cong Y\). Als twee verzameling \(X\) en \(Y\) niet gelijkmachtg zijn, dan noteren we dit met \(X\ncong Y\).

De relatie "is gelijkmachtig aan" is een equivalentierelatie tussen verzamelingen. Dat wil zeggen dat voor willekeurige verzamelingen \(X\),\(Y\) en \(Z\):

\(X\cong X\);
Als \(X\cong Y\), dan \(Y\cong X\);
Als \(X\cong Y\) en \(Y\cong Z\), dan \(X\cong Z\).

\(X\cong X\) (reflexiviteit): de identieke afbeelding \(\mathrm{id}_X:\;X\rightarrow X\) gedefinieerd door \(\mathrm{id}(x)=x\) voor alle \(x\in X\) is een bijectie;
Als \(X\cong Y\), dan \(Y\cong X\) (symmetrie): als \(f\:\;X\rightarrow Y\) bijectie is, dan is de inverse functie \(f^{-1}\:\;X\rightarrow Y\) dat ook;
Als \(X\cong Y\) en \(Y\cong Z\), dan \(X\cong Z\) (transitiviteit): als \(f\:\;X\rightarrow Y\) een bijectie is en \(g\:\;Y\rightarrow Z\) en bijectie is, dan is de samenstelling \(g\circ f\:\;X\rightarrow Z\) ook een bijectie.

Voorbeelden

\(\{a,b,c\}\cong \{1,2,3\}\)
want de functie \(f\) gedefinieerd door \(f(a)=1\), \(f(b)=2\), \(f(3)=c\) is een bijectie van \(\{a,b,c\}\) naar \(\{1,2,3\}\).
\(\{a,b,c,d\}\ncong \{1,2,3\}\)
want het duiventil principe garandeert dat er geen injectieve functie van \(\{a,b,c,d\}\) naar \(\{1,2,3\}\) bestaat, laat staan een bijectie.
Het gesloten interval \([0,1]\) in \(\mathbb{R}\) is gelijkmachtig aan elk ander gesloten interval \([a,b]\) (met \(a<b\))
want de functie \(f\) gedefinieerd door \(f(x)=(b-a)x+a\) is een bijectie van \([0,1]\) naar \([a,b]\).
Het open interval \((-1,1)\) is gelijkmachtig met \(\mathbb{R}\)
want de functie \(f:\;(-1,1)\rightarrow \mathbb{R},\quad f(x)=\tan(\tfrac{1}{2}\pi x)\) is een bijectie van \((-1,1)\) naar \(\mathbb{R}\).
\(\mathbb{N}\backslash \{0\}\cong \mathbb{N}\)
want de functie \(f\) gedefinieerd door \(f(n)=n-1\) is een bijectie van \(\mathbb{N}\backslash \{0\}\) naar \(\mathbb{N}\). Dit betekent dat het bij tellen van elementen eigenlijk niet uitmaakt of je begint bij \(1\) of \(0\).
\(\mathbb{Z}\cong \mathbb{N}\) want de functie \(f(n)=\begin{cases}2n&\text{if }n\ge 0\\ -2n-1&\text{if }n< 0\end{cases}\) is een bijjectie van \(\mathbb{Z}\) naar \(\mathbb{N}\).

Een formele definitie van eindigheid en oneindigheid van een verzameling is als volgt:

Een verzameling \(X\) heet:

eindig als er een \(n\in \mathbb{N}\) bestaat zodanig dat \(X\cong\{0,\ldots , n-1\}\) (waarbij \(\{\}=\emptyset\)).
Het aantal elementen van \(X\), dat we deftig de cardinaliteit van \(X\) noemen, is dan gelijk aan \(n\) en we noteren dit als \(|X|=n\);
oneindig als \(X\) niet eindig is.
Voorbeelden van niet-eindige verzamelingen zijn de getallenverzamelingen \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) en \(\mathbb{R}\)

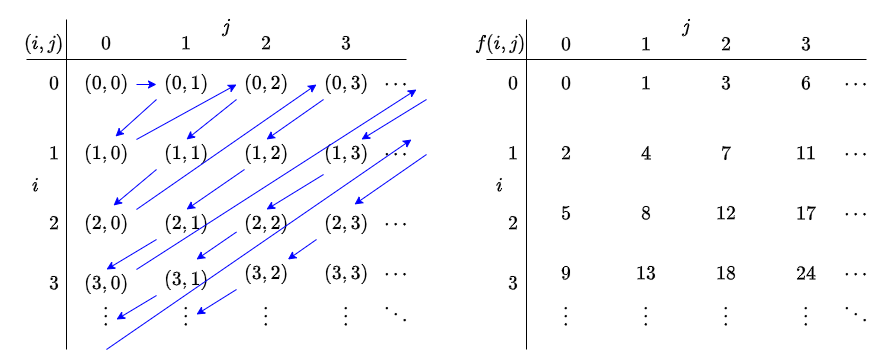
\(\mathbb{N}\times \mathbb{N} \cong \mathbb{N}\).

In onderstaand diagram staan links de elementen van \(\mathbb{N}\times \mathbb{N}\) in een rooster samen met blauwe pijlen die aangeven in welke volgorde we de elementen van de verzameling gaan afwandelen. Rechts staat dan de telling van de elementen volgens deze wandeling langs diagonalen beginnend bij \(0\).

wandeling langs diagonalen

Op plek \((i,j)\) komen we langs met het telnummer gegeven door de functie \(f\) gedefinieerd door \(f(i,j)=\tfrac{1}{2}(i+j)(i+j+1)+i\). Dit is een bijectie van \(\mathbb{N}\times \mathbb{N}\) naar \(\mathbb{N}\).

Zonder bewijs:

\(\mathbb{R} \cong {\Large\wp}(\mathbb{N})\).