Solving quadratic inequalities via reduction and/or factorisation

Solving quadratic equations and inequalities: Quadratic inequalities

Solving quadratic inequalities via reduction and/or factorisation

The steps in solving a quadratic inequality with one unknown via reduction are the same as in solving a quadratic equation by reduction:

addition or subtraction of the same term on both sides;
multiplication or division by the same nonzero number on both sides;
Combination of similar terms.

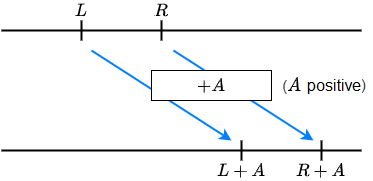
\(L<R\) is equivalent to
\(L+A<R+A\) and \(L-A<R-A\)

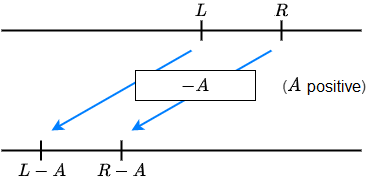
\(L>R\) is equivalent to
\(L+A>R+A\) and \(L-A>R-A\)

Here, \(A\) is an arbitrary expression.

Example
\[\begin{aligned} 4x^2+1&>5\\[0.25cm] 4x^2+1-1&>5-1\\[0.25cm] 4x^2&>4\end{aligned}\]

Inequalities ≤ or ≥ The rule also applies to inequalities \(\le\) or \(\ge\); In fact, this involves a combination of an inequality \(\lt\) or \(\gt\) and a quadratic equation, for which the rule also holds. For example: \[\begin{aligned} 4x^2+1&\ge 5\\[0.25cm] 4x^2+1-1&\ge 5-1\\[0.25cm] 4x^2&\ge 4\end{aligned}\]

Whether or not an equivalence symbool The reduction is based on equivalence of inequalities and you can use the double implicaton arrows \(\Leftrightarrow\). You write for example \[\begin{aligned} 4x^2+1 \ge 5 &\Leftrightarrow 4x^2+1-1 \ge 5-1\\[0.25cm] &\Leftrightarrow 4x^2\ge 4\\[0.25cm]&\Leftrightarrow x^2\ge 1\end{aligned}\] But because of the stepwise structured reduction it is often enough to place consecutive equivalent expressions on separate lines, omitting the equivalence symbol. Then you get \[\begin{aligned} 4x ^ 2 + 1 &\ge 5 \\[0.25cm] 4x^2+1-1&\ge 5-1\\[0.25cm] 4x^2&>4\\[0.25cm] x^2&>1\end{aligned}\]

Visualisation If you substitute a solution for \(x\) in the inequality \(L<R\), then \(L\) and \(R\) become numbers, of which \(L\) is to the left of \(R\) on the number line. When you add or subtract on both sides of the inequality a number \(A\) nothing changes in the relative position of the numbers.

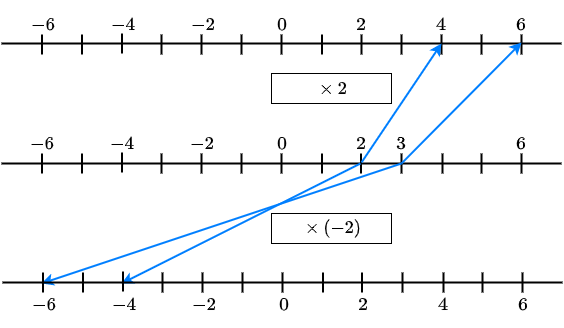
If \(A>0\), then \(L<R\) is equivalent to
\(A\cdot L<A\cdot R\) and \(\dfrac{L}{A}<\dfrac{R}{A}\)

If \(A>0\), then \(L>R\) is equivalent to
\(A\cdot L>A\cdot R\) and \(\dfrac{L}{A}>\dfrac{R}{A}\)

If \(A<0\), then \(L<R\) is equivalent to
\(A\cdot L>A\cdot R\) and \(\dfrac{L}{A}>\dfrac{R}{A}\)

If \(A<0\), then \(L>R\) equivalent is to
\(A\cdot L<A\cdot R\) and \(\dfrac{L}{A}<\dfrac{R}{A}\)

Here, \(A\) is an arbitrary nonzero number.

Examples
\[\begin{aligned} -x^2&< 1\\[0.25cm] (-1)\cdot (-x^2)&\gt(-1)\cdot 1\\[0.25cm] x^2&\gt -1\\[0.75cm]-2x^2&>8\\[0.25cm]\dfrac{-2x^2}{-2}&<\dfrac{8}{-2}\\[0.25cm] x^2&<4\end{aligned}\]

Inequalities ≤ or ≥ The rule also applies to inequalities \(\le\) or \(\ge\); In fact, this involves a combination of an inequality \(\lt\) or \(\gt\), and a linear equation, for which the rule applies too.
Thus, when multiplying or dividing by a negative number, the inequality sign \(\le\) is replaced by \(\ge\), and\(\ge\) is replaced by \(\le\); The inequality sign 'flips'. For example: \[\begin{aligned} -x^2&\le 1\\[0.25cm] (-1)\cdot (-x^2)&\ge(-1)\cdot 1\\[0.25cm] x^2&\ge -1\\[0.75cm]-2x^2&\ge -8\\[0.25cm]\dfrac{-2x^2}{-2}&\le\dfrac{-8}{-2}\\[0.25cm] x^2&\le 4\end{aligned}\]

visualization

If you substitute a solution for \(x\) in the inequality \(L<R\), then \(L\) and \(R\) become numbers, of which \(L\) is to the left of \(R\) on the number line. When you multiply the two numbers by a number \(A\) or divide by \(A\), it depends on the sign of \(A\) whether or not the relative position of the numbers on the number line changes.

For example, suppose that you get after substitution of\(x\) the numbers \(L=2\) and \(R=3\). Then you have \(L<R\) and \(L\) is located on the number line to the left of \(R\). If you multiply the left and right in the inequality by \(2\), you get \(4<6\) and that is true. But if you had instead multiplied the left-hand and right-hand side in the inequality by \(-2\) you would have gotten \(-4<-6\) and that is incorrect; The true statement is \(-4>-6\) and the inequality sign 'flips' because the number that was first to the left on the number line has now become a number to the right.

With the above rules, you can solve quadratic inequalities, i.e., reduce to an inequality in which the unknown is isolated and on the left-hand side of a inequality. Completing the square and factorisation by inspection are often productive strategies.

Solving quadratic inequalities by completing the square Suppose that reduction and completing the square has led to the inequality \[a(x+p)^2+q<0\] for certain real numbers \(a\), \(p\), \(q\) with\(a\neq 0\).

If \(a>0\), then this is equivalent to the inequality \((x+p)^2<\dfrac{q}{a}\). We distinguish three cases:

if \(q<0\), then there are no solutions.
as \(q=0\), then \(x=-p\) is the only solution.
as \(q>0\), then \(-\sqrt{\dfrac{q}{a}}<x+p<\sqrt{\dfrac{q}{a}}\), that is \(-p-\sqrt{\dfrac{q}{a}}<x<-p+\sqrt{\dfrac{q}{a}}\)

If \(a<0\) then this is equivalent to the inequality \((x+p)^2>\dfrac{q}{a}\). We distinguish three cases:

if \(q<0\) then all real numbers satisfy the inequalite because a square of a real number is always greater than or equal to \(0\).
as \(q=0\), then \(x=-p\) the only solution.
as \(q>0\), then \(x+p<-\sqrt{\dfrac{q}{a}}\;\vee x+p>\sqrt{\dfrac{q}{a}}\), that is \(x<-p-\sqrt{\dfrac{q}{a}}\;\vee\;x<-p+\sqrt{\dfrac{q}{a}}\)

Solving a quadratic inequality via factorisation by inspection Suppose that you can write the inequality as \[a(x+p)(x+q)>0\] for certain real numbers \(a\), \(p\), \(q\) with \(a\neq 0\).

If \(a>0\), then this is equivalent to the inequality \((x+p)(x+q)>0\). We distinguish two cases:

if \(x+p>0\) and \(x+q>0\), then \(x>-p\) and \(x>-q\), that is \(x>\max(-p,-q)\).
if \(x+p<0\) and \(x+q<0\), then \(x<-p\) and \(x<-q\), that is \(x<\min(-p,-q)\).

If \(a<0\), then the inequality is equivalent to \((x+p)(x+q)<0\) with solution \(\min(-p,-q)<x<\max(-p,-q)\).

Illustrative examples:

Determine the exact real solution of the following quadratic inequality by completing the square. \[4x^2+12x+28<0\]

We work out the method of completing the square: \[\begin{aligned} 4x^2+12x+28<0 & \phantom{abcxyz} \blue{\text{the given quadratic inequality}} \\ \\ x^2+3x+7<0 & \phantom{abcxyz} \blue{\text{division by }4\text{ on both sides}} \\ \\ \left(x+{{3}\over{2}}\right)^2-\left({{3}\over{2}}\right)^2+7<0 &\phantom{abcxyz} \blue{\text{completing the square}}\\ \\ \left(x+{{3}\over{2}}\right)^2+{{19}\over{4}}<0& \phantom{abcxyz} \blue{\text{simplification}}\\ \\ \left(x+{{3}\over{2}}\right)^2<-{{19}\over{4}}& \phantom{abcxyz} \blue{\text{isolation of the square term}}\\ \\ \text{no solution} & \blue{\phantom{abcxyz}\text{the square of a real number cannot be negative}} \end{aligned}\]

New example