Calculating with numbers: Calculating with fractions
 Rational numbers
Rational numbers
Natural number and integers The sequence \(0, 1,2,3,\ldots\) is the sequence of natural numbers. These are the numbers used to count a finite number of objects. The set of natural numbers is denoted by \(\mathbb{N}\)
Calculating with natural numbers goes well if you add the numbers. But subtracting natural numbers causes problems. For example, what is the result of \(1-2\) or \(2-3\)? This leads to the introduction of the set of integers, denoted by \(\mathbb{ℤ}\)
The integers can be drawn on a number line: start with a first point on a straight line and give it the label 0 and choose a second point that gets the label 1. We agree on the distance between these two points being equal to 1. Now make strides with size 1 along the number line and always label the next position with the next integer. Do the same in the other direction and you get the following number line:
![]()
Rational numbers In \(\mathbb{ℤ}\) we can add, subtract, and multiply without problems. But the division of two integers not always produces an integer value. This leads to the introduction of the set of rational numbers, denoted by \(\mathbb{Q}\)
Also, the rational numbers, i.e., the numbers that can be written as a fraction, can be placed on the number line. In the drawing below, you can see the construction of some of these points.
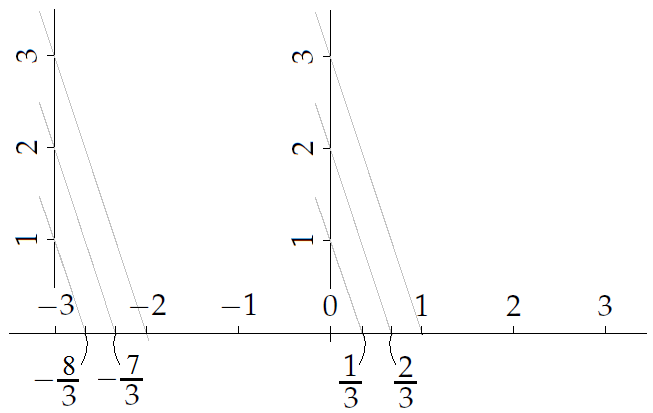
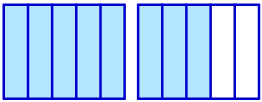
In a fraction there are two integers, the numerator and the denominator, separated by a horizontal or slanted line. In the above picture, a rational number is drawn on the number line that as fraction \(\tfrac{2}{3}\) has numerator \(2\) and denominator \(3\). But we could also have linked the point with label 6 on the vertical line passing through 0 with the point on the horizontal number line with label 1 and have drawn parallel lines. Then we would have given the point with the previous label \(\tfrac{2}{3}\) instead the label \(\tfrac{4}{6}\).
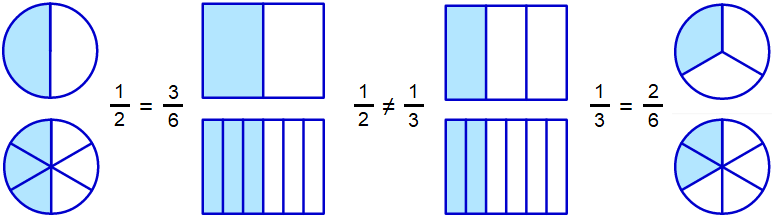
In other words, the representation of a rational number as a fraction is not unique: For example, \(\tfrac{2}{3}\) and \(\tfrac{4}{6}\) represent the same rational number and we write \(\tfrac{2}{3}=\tfrac{4}{6}\) In general, we have the following rewrite rule.
Rewriting fractions When you multiple or divide the numerator and denominator of a fraction with the same (nonzero) integer, then the value of the fraction does not change.
Dividing the numerator and denominator of a fraction by the same factor greater than 1 is called simplifying the fraction. For example, \(\tfrac{4}{6}\) can be simplified to \(\tfrac{2}{3}\) by dividing both the numerator and denominator by 2. We speak of an irreducible fraction or a fraction in lowest terms if the greatest common divisor (gcd) of the numerator and denominator is equal to 1, i.e., the numerator and denominator do not have a common divisor anymore.
Fractions with a common denominator We speak of fractions with a common denominator when they have the same denominator. Two fractions can always be reduced to the same denominator by multiplying the numerator and denominator in each fraction by the same factor so that all denominators become the same. Taking the least common multiple (lcm) of the original denominators yields the simplest fraction with a common denominator.
Here we first claculated the least common multiple (lcm) of the two denominators \((\)in this case, \(\mathrm{lcm}(10,15)=30)\) and then adjusted the numerators and denominators accordingly.
Real numbers Besides rational numbers still other numbers can be constructed on the number line by ruler and compass. For example, the number \(\sqrt{2}\). All numbers together form the set of real numbers, denoted by \(\mathbb{R}\). A real number that is not rational is called an irrational number. Well-known irrational numbers are \(\sqrt{2}\), \(\pi\approx 3.141592\ldots\) and the base of the natural logarithm \(e\approx 2.71828\ldots\).
Matchcentre video clips
Basic Ideas (26:01)

 \(\phantom{abcdabcd}\)
\(\phantom{abcdabcd}\) 
 \(\phantom{abcdabcd}\)
\(\phantom{abcdabcd}\)