Calculating with letters: Computing with letters
 Basic rules
Basic rules
Apply priority rules when you calculate with numbers.
Priority rules
- Addition and multiplication are applied in the order in which they occur, from left to right.
- Multiplication, and division are applied in the order in which they occur, from left to right.
- Multiplication and division have priority over addition and subtraction.
- Exponentiation has priority over multiplication and division
"Please Excuse My Dear Aunt Sally" (PEMDAS) is a mnemonic in the USA to remember some priority rules for calculation: first Parenthesis, then Exponents, hereafter Multiplication, followed by Division, and finally Addition and Subtraction. In other countries similar mnemonics are used: for instance, BIDMAS used in the UK stands for the order Brackets, Indices, Division, Multiplication, Addition, Subtraction
With brackets you can change the normal order of operation.
\[\begin{aligned}6-3+2&= (6-3)+2=5\\ 6-(3+2)&= 1\\6-3\times 2&= 6-(3\times 2)=0\\ (6-3)\times 2&= 6\\ 6\div 3\times 2 &= (6\div 3)\times 2=4\\ 6\div(3\times 2&= 13-2 \end{aligned}\]
Variable When you replace the numbers in an arithmetic expression by letters, than you get an algebraic expression. The letters are then like slots for numbers. But they can be symbols for a variable quantity, for example the letter \(T\) for temperature or \(t\) for time. Such a letter is called a variable.
The same priority rules are applied in calculations with letters. After all, when you fill in values for the variables, you must be able to interpret the result of substitution as a calculation with number. You can also calculate with letters and for example call \(x+y\) the sum of \(x\) and \(y\), or call \(2x\) the doubling of \(x\).
But you must be careful in what you do when you substitute numbers and not simply replace for example \(x\) in \(2x\) by \(4\): substitution of \(x=4\) in \(2x\) is not equal to \(24\), but results in this example in the number \(8\). When substituting negative number, place brackets when needed: substitution of \(x=-3\) in \(x^2\) is not equal to \(-3^2\), but equal to \((-3)^2\).
The following notational agreements are used when calculating with letters.
Notational conventions
- Because the multiplication symbol \(\times\) resembles too much the letter \(x\) it is often replaced in formulas by a point \(x\cdot y\) or it is completely omitted \(xy\) when no confusion can arise.
- In mixed forms of numbers and letters, for example \(2xy^3\) , it is common to first write the coefficient: so \(2xy^3\) and not \(x2y^3\) .
- If the notation leaves room for different interpretations or an expression simply is hard to read, one often uses brackets and points as multiplication sign: \(2xy^3\) is by convention \(2\cdot x\cdot\ y^3\) and not equal to \(2(xy)^3\) or \((2ab)^3\) .
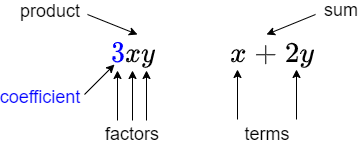
The expression \(2xy\) is a product and the number \(2\) is called the coefficient of \(xy\).
The expression \(x+2y\) is a sum with the termen \(x\) and \(2y\). The number \(2\) is the coefficient of the term \(2y\).
For any variable \(x\) and any positive integer \(k\) we have: \[\begin{aligned} x^k&=\blue{ \overbrace{\color{black}{x \times x \times \cdots \times x}}^{k\mathrm{\;times}}} \\ x^0\; & = 1 \\ x^{-k}\; & = \frac{1}{x^k} \end{aligned}\]
Herewith we defined \(x^n\) for any integer \(n\). The number \(n\) is called the exponent. Instead of \(x^1\) we write \(x\), and we agree on \(x^0=1\).
![]()
Examples
\[\begin{aligned}(2x)^3 &= 8x^3\\[0.2cm] x^{-1}&=\frac{1}{x}\\[0.2cm] \frac{1}{2}x^{-3} &=\frac{1}{2x^3}\end{aligned}\]
For any variable \(x\) and any positive integers \(m\) and \(n\) we have: \[ \sqrt[n]{x^m} =x^{\frac{m}{n}}\]
Herewith we defined \(x^r\) for any positive rational \(r\). The number \(r\) is called exponent. We agree on \[x^{-r}=\frac{1}{x^r}\] and then we have defined the power of any fraction as exponent. We call such expressions radical expressions or roots.
Examples
\[\begin{aligned}\sqrt{x} &= x^{\frac{1}{2}}\\[0.2cm] \sqrt[5]{x^3}&=x^{\frac{3}{5}}\\[0.2cm] \frac{1}{\sqrt{x}} &=x^{-\frac{1}{2}}\\[0.2cm] \frac{1}{4}x^{-\frac{2}{3}} &=\frac{1}{4\sqrt[3]{x^2}}\end{aligned}\]
Simplification
The expression \(2\cdot 3x\) can be simplified into \(6x\). The expression \(3x+4x-5x\) becomes less wieldy when you replace it by \(2x\). Making an algebraic expression more simple and shorter is referred to as simplification.
In simplification of algebraic expression you often use the commutative, associative, and distributive properties to
- do calculations with numbers;
- collect similar terms, i.e. terms with the same letters and exponents;
- alphabetically order letters and placing numbers in front.
Examples
\[\begin{aligned}2x+3+4x-5 &= 6x-2\\[0.2cm]
y\cdot 2x\cdot 3y &= 6xy^2\\[0.2cm]
\frac{xy^2}{2y}&=\tfrac{1}{2}xy\\[0.2cm]
x^2 + 2x + 3x^2 + x^3 &=x^3+4x^2+2x\\[0.2cm]
(2x+3x)4x &= 20x^2\\[0.2cm](-2xy^3)^4&=16x^4y^{12}\end{aligned}\]
&=-8t^2&\blue{\text{calculation of the final result}}\end{aligned}\]
Mathcentre videos
Rules of Arithmetic (29:07)
#\phantom{x}#
Substitution in Formulae (20:58)
#\phantom{x}#
Mathematical Language (21:24)


