Solving a linear inequality by reduction

Solving linear equations and inequalities: Linear inequalities in one unknown

Solving a linear inequality by reduction

The steps in solving linear inequality in one unknown by reduction are the same as in solving a linear equation by reduction:

adding or subtracting the same term on both sides of an equality;
multiplying or dividing by the same number on both sides of an equality;
combining similar terms.

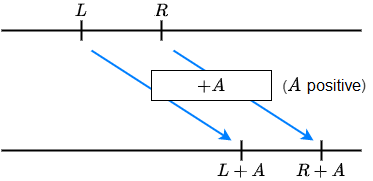
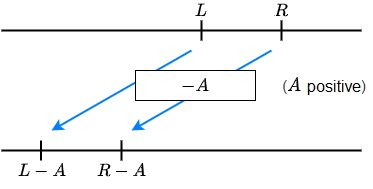
\(L<R\) is equivalent to
\(L+A<R+A\) and \(L-A<R-A\)

\(L>R\) is equivalent to
\(L+A>R+A\) and \(L-A>R-A\)

Here, \(A\) is an arbitrary expression.

example
\[\begin{aligned} 2x+3&>4\\[0.25cm] 2x+3-3&>4-3\\[0.25cm] 2x&>1\end{aligned}\]

Inequalities with ≤ or ≥ The rule also applies to inequalities with \(\le\) or \(\ge\); In fact, this involves a combination of an inequality \(\lt\) or \(\gt\) and a linear equation, for which the rule applies. For example: \[\begin{aligned} 2x+3&\ge4\\[0.25cm] 2x+3-3&\ge4-3\\[0.25cm] 2x&\ge 1\end{aligned}\]

With or with an equivalence symbol The reduction is based on equivalence of inequalities and the use of the equivalence symbol \(\Leftrightarrow\) is applicable. You write in the example \[\begin{aligned} 2x+3>4 &\Leftrightarrow 2x+3-3>4-3\\[0.25cm] &\Leftrightarrow2x>1\end{aligned}\] But because of the stepwise structured reduction it is often enough to place consecutive equivalent expressions on separate lines, omitting the equivalence symbol. Then you get \[\begin{aligned} 2x+3&>4\\[0.25cm] 2x+3-3&>4-3\\[0.25cm] 2x&>1\end{aligned}\]

Visualisation If you substitute a solution for \(x\) in the inequality \(L<R\), then \(L\) and \(R\) become numbers, of which \(L\) is to the left of \(R\) on the number line. When you add or subtract on both sides of the inequality a number \(A\) nothing changes in the relative position of the numbers.

If \(A>0\), then \(L<R\) is equivalent to
\(A\cdot L<A\cdot R\) and \(\dfrac{L}{A}<\dfrac{R}{A}\)

If \(A>0\), then \(L>R\) is equivalent to
\(A\cdot L>A\cdot R\) and \(\dfrac{L}{A}>\dfrac{R}{A}\)

If \(A<0\), then \(L<R\) is equivalent to
\(A\cdot L>A\cdot R\) and \(\dfrac{L}{A}>\dfrac{R}{A}\)

If \(A<0\), then \(L>R\) equivalent is to
\(A\cdot L<A\cdot R\) and \(\dfrac{L}{A}<\dfrac{R}{A}\)

Here, \(A\) is an arbitrary nonzero number.

Examples
\[\begin{aligned} -x&< 1\\[0.25cm] (-1)\cdot (-x)&\gt(-1)\cdot 1\\[0.25cm] x&\gt -1\\[0.75cm]-2x&>4\\[0.25cm]\dfrac{-2x}{-2}&<\dfrac{4}{-2}\\[0.25cm] x&<2\end{aligned}\]

Inequalities with ≤ or ≥ The rule also applies to inequalities \(\le\) or \(\ge\); in fact, this involves a combination of an inequality \(\lt\) or \(\gt\), and a linear equation, for which the rule applies as well.
Thus in multiplication or division by a negative number the inequality sign \(\le\) is replaced by \(\ge\), and\(\ge\) is replaced by \(\le\); The inequality sign 'flips'. For example: \[\begin{aligned} -x&\le 1\\[0.25cm] (-1)\cdot (-x)&\ge(-1)\cdot 1\\[0.25cm] x&\ge -1\\[0.75cm]-2x&\ge4\\[0.25cm]\dfrac{-2x}{-2}&\le\dfrac{4}{-2}\\[0.25cm] x&\le2\end{aligned}\]

Visualisation

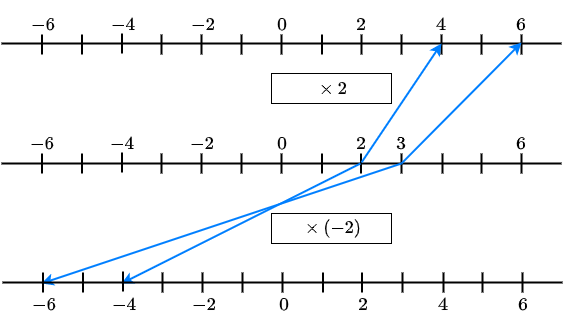
If you substitute a solution for \(x\) in the inequality \(L<R\), then \(L\) and \(R\) become numbers, of which \(L\) is to the left of \(R\) on the number line. When you multiply the two numbers by a number \(A\) or divide by \(A\), it depends on the sign of \(A\) whether or not the relative position of the numbers on the number line changes.

For example, suppose that you get after substitution of\(x\) the numbers \(L=2\) and \(R=3\). Then you have \(L<R\) and \(L\) is located on the number line to the left of \(R\). If you multiply the left and right in the inequality by \(2\), you get \(4<6\) and that is true. But if you had instead multiplied the left-hand and right-hand side in the inequality by \(-2\) you would have gotten \(-4<-6\) and that is incorrect; the true statement is \(-4>-6\) and the inequality sign 'flips' because the number that was first to the left on the number line has now become a number to the right.

With the above rules, you can solve linear inequalities, that is, reduce them to inequalities in which the unknown is isolated and is on the left-hand side of an inequality.

In general, the solutions of \(ax+b<0\) with unknown \(x\) can be found as follows.

\(\;\) case	\(\;\) solutions
\(\;a>0\;\)	\(\;x<−\frac{b}{a}\;\)
\(\;a<0\;\)	\(\;x>−\frac{b}{a}\;\)
\(\;a=0\) and \(b\ge 0\;\)	\(\;\) no solution \(\;\)
\(\;a=0\) and \(b<0\;\)	\(\;\) any real number \(x\;\)

We explain why. The inequality is \(ax+b<=0\).

\(\;\) case	\(\;\) solutions	\(\;\) statement
\(\;a>0\)	\(\;x<−\frac{b}{a}\;\)	\(\;\) Subtract \(b\) from both sides; \(\;\) divide then both sides by \(a\).
\(\;a<0\)	\(\;x>−\frac{b}{a}\;\)	\(\;\) Subtract \(b\) from both side; \(\;\) divide then both sides by \(a\); \(\;\) Because \(a<0\) flips the sign.
\(\;a=0\) and \(b\ge 0\)	\(\;\) no solution	\(\;\) The equation is \(b<0\) and this is \(\;\) not true under the given conditions, \(\;\) regardless of the value of \(x\).
\(\;a=0\) and \(b<0\)	\(\;\) any real number \(x\)	\(\;\) The equation is \(b<0\) \(\;\) and this is true for every \(x\) \(\;\) under the given conditions.

Empty set of solutions Instead of the conclusion that there is no solution of an inequality, we also speak of an empty solution set. An empty set is denoted by \(\{\}\) or \(\emptyset\).

You do not need to memorise the above rule, and the ones belonging to other inequality symbols, because the solutions are easy to find by reduction.

Find the exact solution of the following inequality \[-4x \ge 1\]

\(x \le -\frac{1}{4}\)

After all, \[\begin{aligned} -4x &\ge 1 &\quad \blue{\text{the given inequality}} \\ \\ \frac{-4x}{-4} &\le \frac{1}{-4} &\quad \blue{\text{division by }-4\text{ and because }-4<0\\ \text{the inequality symbol is reversed}} \\ \\ x & \le -\frac{1}{4} &\quad\blue{\text{simplification}}\end{aligned}\]

New example