4. Probability Distributions: Practical 4
 Binomial random variables
Binomial random variables
The binomial distribution is the distribution that describes the number of successful outcomes from a sequence of independent experiments with two possible outcomes (like flipping a coin, which would give either heads or tails). This distribution has two parameters: 1) the number of experiments that are conducted and 2) the probability to get a successful outcome for a single experiment.
Let's consider two concrete examples.
If you flip a coin #10# times, then the number of times you get 'heads' has a binomial distribution. Coins will have a probability of #0.5# to give heads. So most times you will just get #5# times 'heads', and occasionally the number of heads will be very low (like #0# or #1# time) or high (#8# or #9# times).
The exams for some courses are in the form of 'multiple choice' questions. Let's consider the case that you would have to take an exam with #20# MC questions which each has #4# options. In an extreme case where you wouldn't have learned anything and just filled-in your answers randomly. What would then be the chance to pass the exam with #11# correct answers? In this example, the number of correct answers has a binomial distribution and through the binomial distribution, you can calculate the probability of passing the exam by pure guesswork.
A binomial random variable is discrete since it can only take on positive integer values (#0#, #1#, #2#, etc.). Note that this is different from a normally distributed random variable which is continuous and can take on any real value (#-0.231#, #4.26#, etc.). If a probability distribution is discrete, then the probability density function is called a probability mass function, because it does give actual probabilities to get a specific outcome for the binomial random variable.
The commands in R for the binomial distribution for a random variable #X# are:
dbinom()- to calculate the probability that you get exactly #x# successes (in #n# experiments, where the theoretical probability of success is #p#)pbinom()- to calculate the probability that the number of successes is within a given intervalqbinom()- to calculate threshold values for the number of successes that will be exceeded with a given probability
The common way to specify that a random variable #X# has a binomial distribution, based on #10# experiments, with a theoretical probability of success of #0.5# is as follows.
#X \sim B(10,0.5)#
The following example illustrates how the distribution (the probability mass function) of a random variable #X \sim B(10,0.5)# can be plotted.
Create a plot of the probability mass distribution of a binomial distribution #B(10,0.5)#.
x <- 0:10Now you can use the
dbinom() function to calculate the probability mass at each of these values of #x# (#P(X = x)#) for the specified binomial distribution. These will be your y-values.y <- dbinom(x, size=10, prob=0.5)
The last step is the actual plotting. Here, we used the parameter option
type='h' to specify that vertical bars should be plotted at each of the values for x (like a barplot, but then only with bars at the allowable x-values).plot(x=x, y=y, type='h')
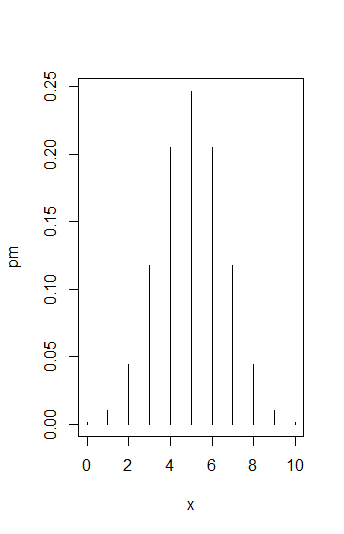
Now, create a plot of the cumulative distribution function for the binomial distributions #B(10,0.5)#.
x <- 1:10Now you use the
pbinom() function to calculate the cumulative probability at each of these values of #x# (#P(X \le x)#) for the specified binomial distributions. These will be your y-values.cp <- pbinom(x, size=10, prob=0.5)Once, you have calculated the x- and y-values, you are ready for plotting!
plot(x=x, y=cp, type='s')
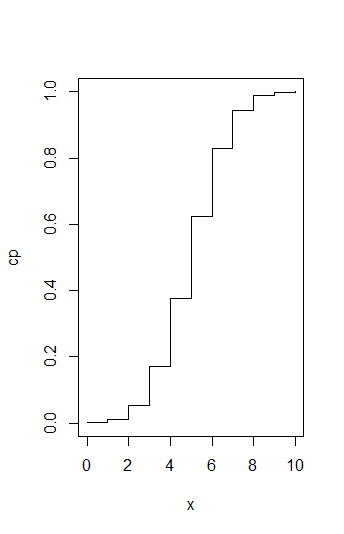
In this graph, the parameter option
type='s' states that the data should be plotted as a 'staircase plot'. The probabilities add-up in a stepwise fashion. In general, for discrete probability distributions, you would need to specify the plotting options type='h' and type='s' for the probability mass and cumulative probability plots respectively.


