Sampling Distribution of the Sample Proportion

5. Sampling: Sampling Distributions

Sampling Distribution of the Sample Proportion

A type of variable which is commonly studied in statistics is the binary variable.
$\phantom{0}$

Binary Variable

Definition

A binary or dichotomous variable is a categorical variable that can only take on $2$ possible values.

Examples

True/false
Success/failure
Yes/no
On/off

$\phantom{0}$
The mean of a binary variable is mathematically equivalent to the proportion.
$\phantom{0}$

Proportion

Definition

In statistics, a proportion refers to the fraction of a group that possesses a particular characteristic.

The population and sample proportion are denoted $\pi$ and $\hat{p}$ , respectively.

Formula

$\text{proportion}=\cfrac{\text{# of individuals with characterstic}}{\text{total number of individuals}}$

$\phantom{0}$
When using a sample proportion to estimate a population proportion, the sampling distribution of the sample proportion can be used to determine how much estimation error is reasonable to expect.
$\phantom{0}$

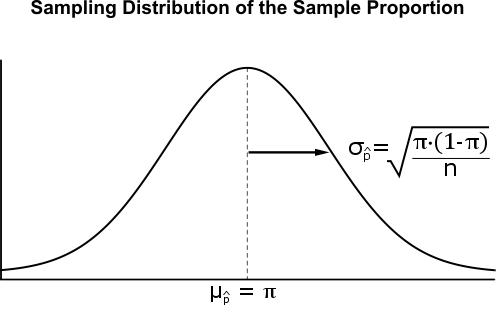
Sampling Distribution of the Sample Proportion

The sampling distribution of the sample proportion is the probability distribution of the sample proportions of every possible sample of a particular size $n$ that can be drawn from a population.

The mean of the distribution of sample proportions is called the expected value of the sample proportion and is denoted $\mu_{\hat{p}}$ .

The standard deviation of the distribution of sample proportions is called the standard error of the sample proportion and is denoted $\sigma_{\hat{p}}$ . The standard error is a measure of how much discrepancy to expect between a sample proportion $\hat{p}$ and the population proportion $\pi$ .

Conditions for Normality

For any population of which a proportion $\pi$ possesses a particular characteristic, the sampling distribution of the sample proportion for samples of size $n$ may be considered approximately normal if both of the following conditions are satisfied:

We expect there to be at least $10$ positive cases: $n \cdot \pi \geq 10$
We expect there to be at least $10$ negative cases: $n \cdot (1-\pi) \geq 10$

If both these conditions are satisfied, the sampling distribution of the sample proportions may be considered approximately normal with parameters:

$\mu_{\hat{p}}=\pi$
$\sigma_{\hat{p}}=\sqrt{\cfrac{\pi \cdot(1-\pi)}{n}}$

$\hat{p} \sim N(\pi, \sqrt{\cfrac{\pi \cdot (1-\pi)}{n}})$

A botanist draws a simple random sample of $160$ flowers from a population of flowers of which a proportion of $\pi = 0.20$ exhibits a particular genetic mutation.

What is the expected value of the sample proportion?

$\mu_{\hat{p}} = 0.20$

Investigate whether the sampling distribution of the sample proportion may be considered approximately normal:

$n\cdot \pi = 160 \cdot 0.20 = 32 \geq 10$
$n\cdot (1-\pi) = 160 \cdot (1-0.20) = 128 \geq 10$

Since both conditions are satisfied, the expected value of the sample proportion, $\mu_{\hat{p}}$ , is equal to the population proportion $\pi$ :

$\mu_{\hat{p}} = \pi= 0.20$

New example