Computing the p-value and Making a Decision

7. Hypothesis Testing: Introduction to Hypothesis Testing

Computing the p-value and Making a Decision

p-value

The $\boldsymbol{p}$ -value of a test is the probability, when the null hypothesis $H_0$ is assumed to be true, of observing a test statistic equal to or more extreme than what was actually observed.

For a two-tailed test, the $p$ -value is a two-tailed probability, which means it is evenly split between both tails.

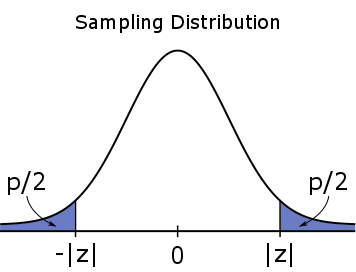
$H_a: \mu \neq \mu_0$

For a one-tailed test, the $p$ -value is a one-tailed probability, which means it is entirely located in one of the tails.

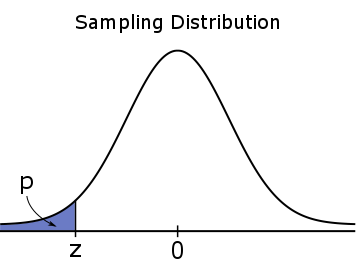
$H_a: \mu \lt \mu_0$

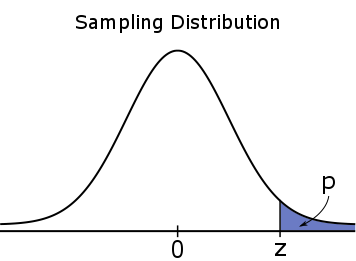
$H_a: \mu \gt \mu_0$

Interpretation of a p-value

The $p$ -value is the probability that the null hypothesis $H_0$ is false. The status of $H_0$ is non-random.

The sample is random, so consequently, the test statistic is also random. Thus the $p$ -value concerns the test statistic.

A small $p$ -value implies that the value of the test statistic is not in the range of values that we would expect if $H_0$ is true.

Calculating the p-value of a z-test for a Population Mean with Statistical Software

The calculation of the $p$ -value of a $z$ -test for $\mu$ is dependent on the direction of the test and can be performed using either Excel or R.

To calculate the $p$ -value of a $z$ -test for $\mu$ in Excel, make use of one of the following commands:

$\begin{array}{lllll} \phantom{0}\text{Direction}&\phantom{0000}H_0&\phantom{0000}H_a&\phantom{000}p\text{-value}&\phantom{0000000000}\text{Excel Command}\\ \hline \text{Two-tailed}&H_0:\mu = \mu_0&H_a:\mu \neq \mu_0&2\cdot \mathbb{P}(Z\geq |z|)&=2 \text{ * }(1 \text{ - }\text{NORM.DIST}(\text{ABS}(z),0,1,1))\\ \text{Left-tailed}&H_0:\mu \geq \mu_0&H_a:\mu \lt \mu_0&\mathbb{P}(Z\leq z)&=\text{NORM.DIST}(z,0,1,1)\\ \text{Right-tailed}&H_0:\mu \leq \mu_0&H_a:\mu \gt \mu_0&\mathbb{P}(Z\geq z)&=1 \text{ - }\text{NORM.DIST}(z,0,1,1)\\ \end{array}$

To calculate the $p$ -value of a $z$ -test for $\mu$ in R, make use of one of the following commands:
$\begin{array}{lllll} \phantom{0}\text{Direction}&\phantom{0000}H_0&\phantom{0000}H_a&\phantom{000}p\text{-value}&\phantom{0000000}\text{R Command}\\ \hline \text{Two-tailed}&H_0:\mu = \mu_0&H_a:\mu \neq \mu_0&2\cdot \mathbb{P}(Z\geq |z|)&2 \text{ * }\text{pnorm}(\text{abs}(z),0,1, \text{FALSE})\\ \text{Left-tailed}&H_0:\mu \geq \mu_0&H_a:\mu \lt \mu_0&\mathbb{P}(Z\leq z)&\text{pnorm}(z,0,1, \text{TRUE})\\ \text{Right-tailed}&H_0:\mu \leq \mu_0&H_a:\mu \gt \mu_0&\mathbb{P}(Z\geq z)&\text{pnorm}(z,0,1, \text{FALSE})\\ \end{array}$

Note: $|z|$ denotes the absolute value of $z$ , i.e. the distance of $z$ from $0$ , regardless of whether $z < 0$ or $z > 0$ .

$\phantom{0}$
Once the $p$ -value of the test has been computed, the time has come to make a decision regarding the null hypothesis $H_0$ .
$\phantom{0}$

Making a Decision

If the computed $p$ -value is smaller than the significance level (i.e. $p \lt \alpha$ ), this means that the observed data is highly unlikely to occur, given that $H_0$ is true. We then say that we reject $H_0$ in favor of $H_a$ .

If the computed $p$ -value is larger than or equal to the significance level (i.e. $p \geq \alpha$ ), this means that the observed data falls in the range of values that we would expect to observe if $H_0$ is true. We then say we do not reject $H_0$ .

The amount of dissolved oxygen in water (mg per liter) is normally distributed with unknown mean $\mu$ and standard deviation $\sigma = 0.78$ .

A researcher collects one-liter water specimens from $200$ randomly-selected locations along a river and measures the amount of dissolved oxygen in each specimen.

The researcher plans on using a $z$ -test to determine if the mean oxygen content of the river significantly differs from $4$ mg per liter, at the $\alpha = 0.02$ level of significance.

The sample mean $\bar{X}$ turns out to be $3.96$ mg per liter.

Calculate the $p$ -value of the test and make a decision regarding $H_0$ . Round your answer to $4$ decimal places.

$p=0.4683$

On the basis of this $p$ -value, $H_0$ should not be rejected, because $\,p$ $\gt$ $\alpha$ .

There are a number of different ways we can calculate the $p$ -value of the test. Click on one of the panels to toggle a specific solution.

Excel Calculation

Because the sample is drawn from a normally-distributed population, we know that the test statistic

$Z=\cfrac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}$

has the $N(0,1)$ distribution, under the assumption that $H_0$ is true.

Calculate the value of test statistic $z$ :

$z = \cfrac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} =\cfrac{3.96 - 4}{0.78/\sqrt{200}} = -0.72524$
For a two-tailed $Z$ -test, the $p$ -value is defined as $2\cdot \mathbb{P}(Z \geq |z|)$ . To calculate this value in Excel, make use of the following function:

NORM.DIST(x, mean, standard_dev, cumulative)

x: The value at which you wish to evaluate the distribution function.

mean: The mean of the distribution.

standard_dev: The standard deviation of the distribution.

cumulative: A logical value that determines the form of the function.

TRUE - uses the cumulative distribution function, $\mathbb{P}(X \leq x)$

FALSE - uses the probability density function

Thus, to calculate $p = 2\cdot \mathbb{P}(Z \geq |z|)$ , run the following command:

$=2 \text{ * }(1 \text{ - } \text{NORM.DIST}(\text{ABS}(z),0,1,1))\\ \downarrow\\ =2 \text{ * }(1 \text{ - } \text{NORM.DIST}(\text{ABS}(\text{-}0.72524),0,1,1))$
This gives:

$p = 0.4683$
Since $\,p$ $\gt$ $\alpha$ , $H_0: \mu = 4$ should not be rejected.

R Calculation

Because the sample is drawn from a normally-distributed population, we know that the test statistic

$Z=\cfrac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}$

has the $N(0,1)$ distribution, under the assumption that $H_0$ is true.

Calculate the value of test statistic $z$ :

pnorm(q, mean, sd, lower.tail)

q: The value at which you wish to evaluate the distribution function.

mean: The mean of the distribution.

sd: The standard deviation of the distribution.

lower.tail: If TRUE (default), probabilities are $\mathbb{P}(X \leq x)$ , otherwise, $\mathbb{P}(X \gt x)$ .

Thus, to calculate $p = 2\cdot \mathbb{P}(Z \geq |z|)$ , run the following command:

$2 \text{ * } \text{pnorm}(q = \text{abs}(z), mean = 0, sd = 1,lower.tail = \text{FALSE})\\ \downarrow\\ 2\text{ * } \text{pnorm}(q = \text{abs}(\text{-}0.72524), mean = 0, sd = 1,lower.tail = \text{FALSE})$
This gives:

$p = 0.4683$
Since $\,p$ $\gt$ $\alpha$ , $H_0: \mu = 4$ should not be rejected.

New example