7. Hypothesis Testing: Introduction to Hypothesis Testing
 Errors in Decision Making
Errors in Decision Making
Inferential statistics makes use of the limited information provided by a sample to draw conclusions about a larger population.
Samples are not expected to be a perfect representation of their population, however, and in some extreme cases the sample will be very different from the population it is drawn from. Such extreme samples can lead to incorrect conclusions about the population.
Remember that there are two possible decisions that can be made on the basis of a hypothesis test:
- The null hypothesis is rejected.
- The null hypothesis is not rejected.
Both of these decisions can either be correct or incorrect, which leads to four possible scenarios.
\[
\begin{array}{l|c|c}
&H_0\text{ is not rejected}&H_0\text{ is rejected}\\
\hline
H_0 \text{ is true}&\green{\text{Correct decision}}&\red{\text{Type I error}}\\
H_0 \text{ is false}&\red{\text{Type II error}}&\green{\text{Correct decision}}\\
\end{array}
\]
Type I Error
A Type I error is rejecting the null hypothesis when, in fact, it is true. This is also known as a false positive result. The probability of committing a Type I error is equal to the significance level of the test and is denoted #\alpha#.
\[\alpha = \mathbb{P}(\text{Type I error})=\mathbb{P}(\text{reject }H_0\,|\,H_0\text{ is true})\]
A Type I error is analogous to an innocent person being found guilty.
#\phantom{0}#
Type II Error
A Type II error is failing to reject the null hypothesis when, in fact, it is false. This is also known as a false negative a result. The probability of committing a Type II error is denoted by #\beta#.
\[\beta = \mathbb{P}(\text{Type II error})=\mathbb{P}(\text{do not reject }H_0\,|\,H_0\text{ is false})\]
A Type II error is analogous to a guilty person being found not guilty.
#\phantom{0}#
The distinction between the two types of errors is illustrated by the following tree diagram: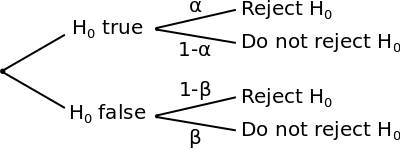
It might be tempting to reduce the chances of committing a Type I error by choosing a very low significance level.
There is a trade-off, however, as decreasing the chances of committing a Type I error simultaneously increases the chances of committing a Type II error, and vice versa.


