6. Parameter Estimation and Confidence Intervals: Estimation
Constructing a 95% Confidence Interval for the Population Mean
To construct a #95\%# confidence interval for the population mean #\mu# we will need to make use of the sampling distribution of the sample mean.
For the purpose of this example, let's assume that the conditions for normality have been met and the sample mean #\bar{X}# (approximately) has the #N(\mu,\sigma/\sqrt{n})# distribution.
#\phantom{0}#
Constructing a 95% Confidence Interval for the Population Mean
Let #Z# be the standardized version of #\bar{X}#, that is:
\[Z = \cfrac{\bar{X} - \mu}{\sigma_{\bar{X}}} =\cfrac{\bar{X} - \mu}{\sigma/\sqrt{n}}\]
Then #Z# has the Standard Normal Distribution, that is #Z\sim N(0,1)#.
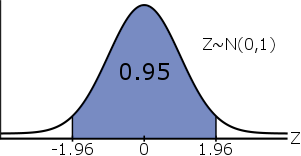
It can be shown#^{1}# that the middle #95\%# of the Standard Normal Distribution falls between #-1.96# and #1.96#:
\[\mathbb{P}(-1.96 \leq Z \leq 1.96) = 0.95\]
Substitituting #Z# with #\cfrac{\bar{X} - \mu}{\sigma/\sqrt{n}}# gives:
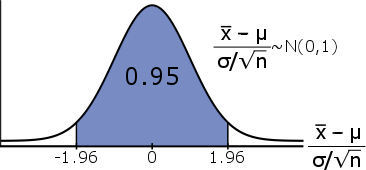
\[\mathbb{P}(-1.96 \leq \cfrac{\bar{X} - \mu}{\sigma/\sqrt{n}} \leq 1.96) = 0.95\]
With the help of a little algebra#^{2}#, this can be rewritten as:
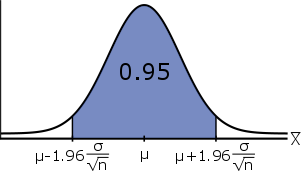
\[\mathbb{P}(\mu -1.96\cdot\cfrac{\sigma}{\sqrt{n}} \leq \bar{X} \leq \mu + 1.96\cdot\cfrac{\sigma}{\sqrt{n}}) = 0.95\]
This result is mathematically equivalent to:
\[\mathbb{P}(\bar{X} -1.96\cdot\cfrac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{X} + 1.96\cdot\cfrac{\sigma}{\sqrt{n}}) = 0.95\]
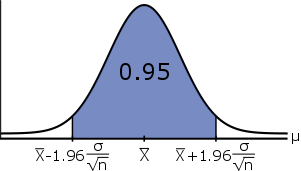
In words, there is a #95\%# probability that we will draw a random sample such that the interval
\[CI_{\mu,95\%}=(L,U)=(\bar{X} -1.96\cdot\cfrac{\sigma}{\sqrt{n}},\,\,\,\, \bar{X} + 1.96\cdot\cfrac{\sigma}{\sqrt{n}})\]
will contain the true value of the population mean #\mu#.
After the sample is drawn and the values of lower bound #L# and the upper bound #U# are computed, the interval #(L,U)# is called a #95\%# confidence interval for #\mu#.
The expression #1.96 \cdot \cfrac{\sigma}{\sqrt{n}}# is called the margin of error, while #95\%# is called the confidence level.
