Direction of a Linear Relationship: Covariance

2. Association and Correlation: Correlation

Direction of a Linear Relationship: Covariance

To determine the direction of the linear relationship between two variables, calculate the covariance.
$\phantom{0}$

Covariance

Definition

The covariance measures the direction of the linear relationship between two quantitative variables.

The sample covariance between two variables $X$ and $Y$ is denoted $s_{\small{X,Y}}$ .

A positive covariance indicates that the variables have a positive linear relationship. A negative covariance indicates that the variables have a negative linear relationship.

Formulas

$s_{\small{X,Y}}=\dfrac{\sum{\bigg((X-\bar{X})(Y-\bar{Y})\bigg)}}{n-1}$

Computation of the Sample Covariance with Statistical Software

To compute the sample covariance between two variables $X$ and $Y$ in Excel, make use of the following function:

COVARIANCE.S(x, y)

x: The numeric vector that contains the values for variable $X$

y: The numeric vector that contains the values for variable $Y$

To compute the sample covariance between two variables $X$ and $Y$ in R, make use of the following function:

cov(x, y)

x: The numeric vector that contains the values for variable $X$

y: The numeric vector that contains the values for variable $Y$

$\phantom{0}$
To calculate the covariance between two variables $X$ and $Y$ , multiply the deviation score with respect to $X$ by the deviation score with respect to $Y$ for each case in the dataset.

If both $X_i$ and $Y_i$ lie on the same side of their respective mean, then the resulting product will be positive, specifically:

If both scores ( $\orange{X_1}$ , $\orange{Y_1}$ ) lie $\orange{\text{below}}$ their respective means then both deviation scores are $\orange{\text{negative}}$ but their product will be positive.
If both scores ( $\purple{X_2}$ , $\purple{Y_2}$ ) lie $\purple{\text{above}}$ their respective means then both deviation scores are $\purple{\text{positive}}$ and so is their product.

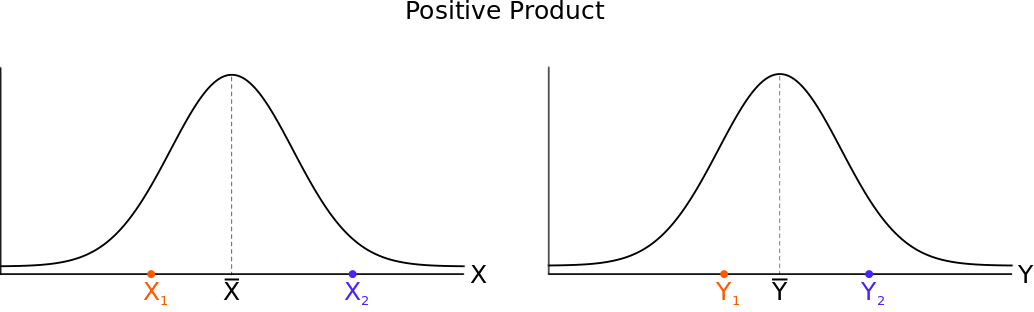
$\phantom{0}$
If the scores lie on opposite sides of their respective means, then one deviation score will be negative ( $\orange{X_3}$ , $\purple{Y_4}$ ) and the other will be positive ( $\orange{Y_3}$ , $\purple{X_4}$ ) and the resulting product will be negative.

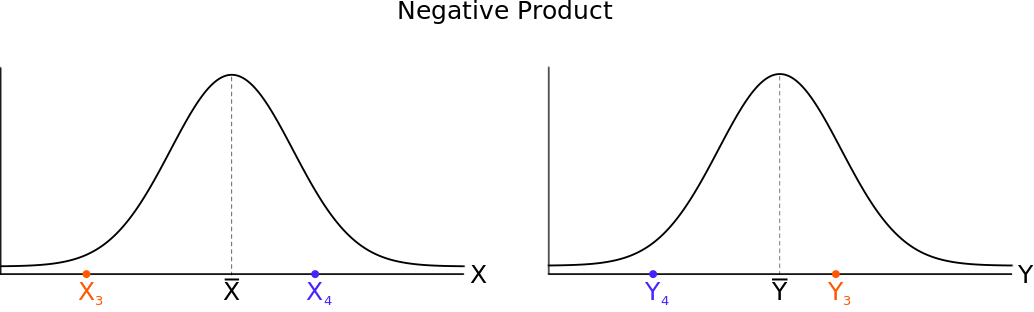
$\phantom{0}$
These products are then averaged and the resulting measure is called the covariance.

Interpreting the sign of the covariance

The sign of the covariance indicates the direction of the linear relationship:

If $s_{\small{X,Y}}>0$ , then $X$ and $Y$ are said to have a positive linear relationship.
If $s_{\small{X,Y}}<0$ , then $X$ and $Y$ are said to have a negative linear relationship.
If $s_{\small{X,Y}}=0$ , then $X$ and $Y$ are said to be linearly unrelated.

Interpreting the magnitude of the covariance

Although the sign of the covariance is a good measure of the direction of the linear relationship between two variables, the magnitude of the covariance is not a good measure of the strength of the relationship. This is because the magnitude of the covariance is heavily dependent on the magnitude of the variables.

Suppose we have a dataset containing the measurements of two variables $X$ and $Y$ . Both of these variables were originally measured in meters. We calculate the covariance between these two variables and find a value of $s_{X,Y}=5$ .

Now suppose we change our mind and decide we want to express the measurements of $X$ and $Y$ in centimeters instead. To do so, we multiply all the values in the dataset by $100$ . We then recalculate the covariance and find a value of $s_{X,Y}=50000$ .

By multiplying each value in the dataset with a factor $100$ , the covariance increased by a factor $100^2$ . This illustrates why the covariance is a poor measure of the strength of the relationship between two variables. Multiplying or dividing all values in our dataset by some value should not affect our measurement of the strength of the relationship between variables.

Consider the following $5$ pairs of data points:

$\begin{array}{|c|c|} \hline X&\,Y\,\\ \hline 5&9\\ 7&4\\ 3&1\\ 8&7\\ 2&4\\ \hline \end{array}$

Calculate the sample covariance between $X$ and $Y$ .

First calculate the means of variables $X$ and $Y$ :
$\begin{array}{rcl} \bar{X}&=&\cfrac{\sum{X}}{n} = \dfrac{5+7+3+8+2}{5}=\dfrac{25}{5}=5\\\\ \bar{Y}&=&\cfrac{\sum{Y}}{n} = \dfrac{9+4+1+7+4}{5}=\dfrac{25}{5}=5 \end{array}$
Now that the means are known, the values of $(X-\bar{X}), (Y-\bar{Y})$ , and $(X-\bar{X})(Y-\bar{Y})$ can be calculated:
$\begin{array}{|c|c|c|c|c|} \hline X&Y&X-\bar{X}&Y-\bar{Y}&(X-\bar{X})(Y-\bar{Y})\\ \hline 5&9&0&4&0\\ 7&4&2&-1&-2\\ 3&1&-2&-4&8\\ 8&7&3&2&6\\ 2&4&-3&-1&3\\ \hline \end{array}$
With this information, the sample covariance can be calculated:

$\begin{array}{rcl} s_{X,Y}&=&\dfrac{\sum\limits_{i=1}^n{(X_i-\bar{X})(Y_i-\bar{Y})}}{n-1}\\ &&\blue{\text{Formula for the sample covariance}}\\ &=&\dfrac{0-2+8+6+3}{5-1}\\ &&\blue{\text{Entered the products from the table and }n \text{ into the equation}}\\ &=&\dfrac{15}{4}\\ &&\blue{\text{Simplified}}\\ &=&3.75\\ \end{array}$

New example