The Pearson correlation coefficient is used to calculate the direction and strength of a linear relationship between two variables. The Pearson correlation coefficient is a 'scaled' version of the covariance, such that it ranges from $-1$ to $+1$. The greater the absolute value of the coefficient, the stronger the relationship.

The scatterplot of two variables gives not only an indication about the form and direction of the relationship; with a little practice, it will also give you an idea about its strength.

Perfect positive linear relationship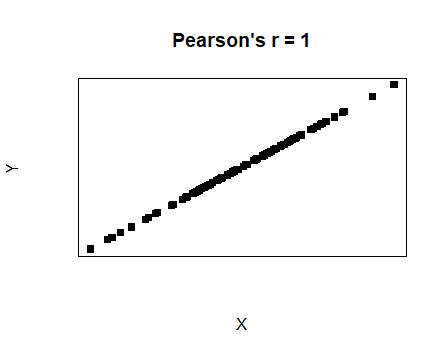
Strong positive linear relationship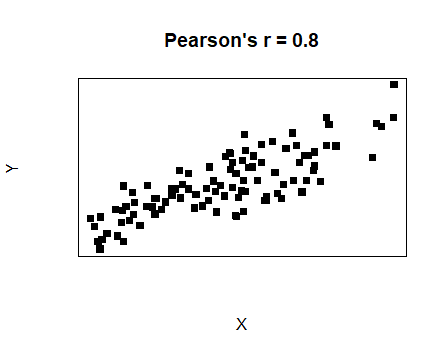
Moderate postive linear relationship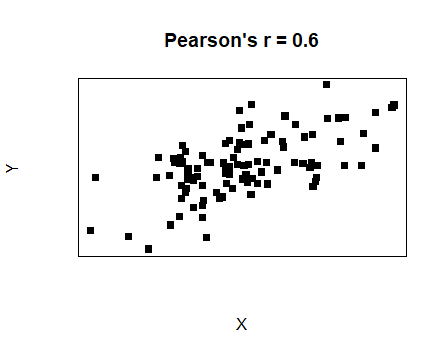
Weak positive linear relationship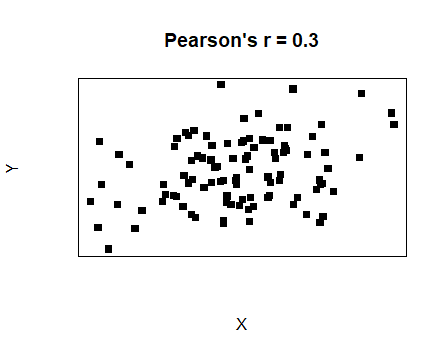
No linear relationship

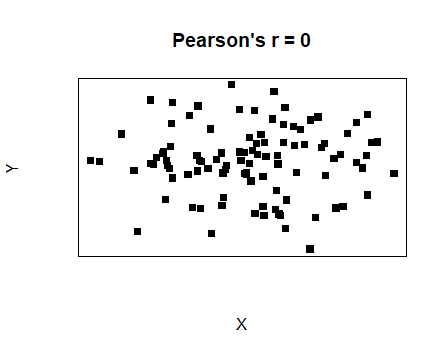Calculate Pearson's correlation coefficient in R

Of course, we can also calculate Pearson's correlation coefficient, instead of only estimating it's strength from the scatterplots. The equation is as follows:

$r(X,Y)=\dfrac{s_{X,Y}}{s_Xs_Y}$,

in which $r(X,Y)$ is Pearson's correlation coefficient for the variables $X$ and $Y$, $s_{X,Y}$ is the covariance between $X$ and $Y$, $s_X$ is the standard deviation of $X$ and $s_Y$ is the standard deviation of $Y$. In R that would translate to

cor_xy <- cov(x,y)/(sd(x)*sd(y))

Alternatively, the correlation coefficient can be calculated by first applying a z-transformation to $X$ and $Y$ and then calculating the covariance. Recall that when we calculate the z-score, we subtract the mean and divide by the standard deviation. We should do that for each observation. Luckily, R has a function that does this for us: scale().

?scale

So $cor(X,Y) = cov(X_z,Y_z)$,
where $X_z = z$-$transformed$ $X$ and $Y_z = z$-$transformed$ $Y$ can be calculated in R with

cor_xy <- cov(scale(x), scale(y))

Lasty, and mosty conviniently, we can calculate the correlation coefficient directly with the cor() function.

cor_xy <- cor(x, y)