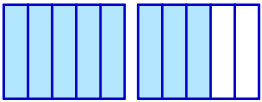
Rekenen met getallen: Rekenen met breuken
 Rationale getallen
Rationale getallen
Natuurlijke en gehele getallen De rij \(0, 1,2,3,\ldots\) is de rij van de natuurlijke getallen. Dit zijn de getallen om een eindig aantal voorwerpen mee te tellen. De verzameling van natuurlijke getallen noteert men met \(\mathbb{N}\).
Het rekenen met natuurlijke getallen gaat goed als je getallen bij elkaar optelt. Maar het aftrekken van getallen geeft problemen. Wat is bijvoorbeeld de uitkomst van \(1-2\) of \(2-3\) ? Dit geeft aanleiding tot de invoering van de verzameling van gehele getallen, aangeduid met \(\mathbb{ℤ}\).
De gehele getallen kun je op een getallenlijn uitzetten: begin met een eerste punt op een rechte lijn en geef dit het naamkaartje 0 en kies een tweede punt dat het naamkaartje 1 krijgt. We spreken af dat de afstand tussen deze twee punten gelijk is aan 1. Schrijd nu voort met passen van lengte 1 en zet steeds een volgend geheel getal als naamkaartje neer. Doe dit ook in de andere richting en je krijgt de volgende getallenlijn:
![]()
Rationale getallen In \(\mathbb{ℤ}\) kunnen we zonder problemen optellen, aftrekken en vermenigvuldigen. Maar het delen van twee gehele getallen levert niet altijd een geheel getal op. Dit geeft aanleiding tot de invoering van de verzameling van rationale getallen, aangeduid met \(\mathbb{Q}\).
Ook de rationale getallen, dat wil zeggen de getallen die als een breuk geschreven kunnen worden, kunnen op de getallenlijn geplaatst worden. In onderstaande tekening staat de constructie van een paar van deze punten.
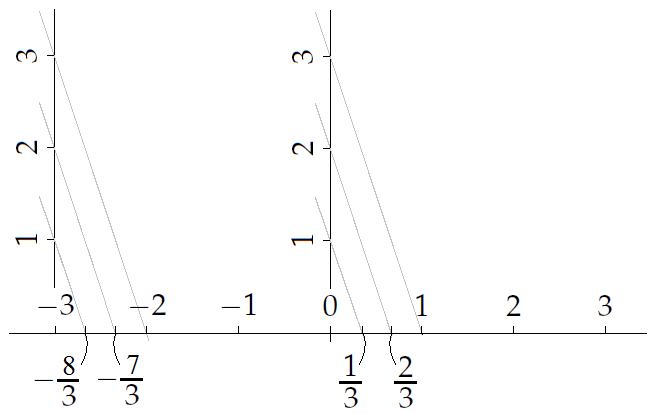
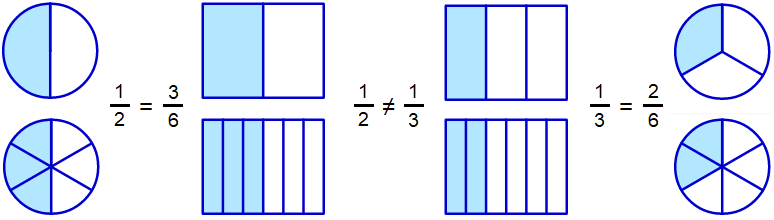
In een breuk staan twee gehele getallen, de teller en de noemer, gescheiden door een horizontale of schuine deelstreep. In bovenstaand plaatje staat een rationaal getal op de getallenlijn getekend dat als breuk \(\tfrac{2}{3}\) met teller \(2\) en noemer \(3\) aangeduid is. Maar we hadden natuurlijk ook het punt met naamkaartje 6 op de verticale lijn door 0 op de horizontale getallenlijn met het punt met naamkaartje 1 op de horizontale lijn kunnen verbinden en parallelle lijnen kunnen tekenen. Dan hadden we het punt met het eerdere naamkaartje \(\tfrac{2}{3}\) ook van het naamkaartje \(\tfrac{4}{6}\) voorzien.
Met andere woorden, de schrijfwijze van een rationaal getal als breuk is niet uniek: \(\tfrac{2}{3}\) en \(\tfrac{4}{6}\) stellen bijvoorbeeld hetzelfde rationale getal voor en we schrijven \(\tfrac{2}{3}=\tfrac{4}{6}\). In het algemeen geldt de volgende herschrijfregel voor breuken.
Herschrijven van breuken Als je de teller en noemer van een breuk met hetzelfde gehele getal (ongelijk aan nul) vermenigvuldigt of deelt, dan verandert de waarde van de breuk niet.
Delen van teller en noemer van een breuk door dezelfde factor groter dan 1 heet vereenvoudigen van de breuk. \(\tfrac{4}{6}\)is bijvoorbeeld te vereenvoudigen tot \(\tfrac{2}{3}\) door de teller en noemer door 2 te delen. We spreken van een onvereenvoudigbare breuk als de grootste gemene deler (ggd) van teller en noemer gelijk aan 1 is, dat wil zeggen, als de teller en noemer onderling ondeelbaar zijn.
Gelijknamige breuken Breuken heten gelijknamig als ze dezelfde noemer hebben. Twee breuken kun je altijd gelijknamig maken door bij elke breuk teller en noemer met dezelfde factor te vermenigvuldigen zodanig dat de noemers aan elkaar gelijk worden. Het zuinigste is het om als gemeenschappelijke noemer het kleinste gemene veelvoud (kgv) van de oorspronkelijke noemers te kiezen.
Het snelst en meest foutenvrij gaat dit door kleinste gemene veelvoud (kgv) van de twee noemers te bepalen. De priemontbindingen van de noemers van de gegeven breuken (van \(10\) en \(13\)) zijn: \[10 = 2\times 5 \qquad\text{en}\qquad 13 =13\quad (13 \text{ is een priemgetal})\] Dit betekent dat \(\mathrm{kgv}(10,13)=2\times 5\times 13=130\).
In de breuk \(\frac{3}{10}\) moeten we de teller en de noemer vermenigvuldigen met \(13\) om op de gelijknamige noemer \(130\) uit te komen. Dan krijgen we: \[\frac{3}{10}= \frac{3\times 13}{10\times 13}=\frac{39}{130}\] In de breuk \(\frac{5}{13}\) moeten we teller en noemer vermenigvuldigen met \(10\) om op de gelijknamige noemer \(130\) uit te komen. Dan krijgen we: \[\frac{5}{13}=\frac{5\times 10}{13\times 10}=\frac{50}{130}\]
Reële getallen Op de getallenlijn zijn nog andere getallen dan rationale getallen te construeren, bijvoorbeeld met passer en liniaal het getal \(\sqrt{2}\). Alle getallen op de getallenlijn vormen samen de verzameling van reële getallen, aangeduid met \(\mathbb{R}\). Een reëel getal dat niet rationaal is noemen we een irrationaal getal. Bekende irrationale getallen zijn \(\pi\approx 3.141592\ldots\) en het grondtal van de natuurlijke logaritme \(e\approx 2.71828\ldots\)
Matchcentre video clips
Basic Ideas (26:01)

 \(\phantom{abcdabcd}\)
\(\phantom{abcdabcd}\) 
 \(\phantom{abcdabcd}\)
\(\phantom{abcdabcd}\)