Natuurlijke en gehele getallen

Rekenen met getallen: Rekenen met gehele getallen

Natuurlijke en gehele getallen

Bij het tellen van voorwerpen start je meestal met \(1\) en ga je door met steeds \(1\) er bij op te tellen. Zo krijg je achtereenvolgens de getallen \(1,\;\;2=1+1,\;\; 3=2+1=1+1+1\), enzovoorts. Om ook de absentie van een voorwerp aan te geven is het getal \(0\) nodig. We kunnen ook vanaf \(0\) terug tellen en dan krijgen we achtereenvolgens de getallen \(-1=0-1,\;\; -2=-1-1,\;\;-3=-2-1=-1-1-1\), enzovoorts. Op deze manier kunnen we alle gehele getallen construeren.

Natuurlijke getallen De rij \(0, 1, 2, 3, \ldots\) is de rij van de natuurlijke getallen. Dit zijn de getallen om mee te tellen of te indexeren. De verzameling van natuurlijke getallen noteert men met \(\mathbb{N}\). Dus \[\mathbb{N}=\{0,1,2,3,\ldots\}\]

Wel of niet 0 erbij Je kunt er over discussiëren of het getal 0 bij de natuurlijke getallen hoort: bij het tellen van voorwerpen begin je immers te tellen vanaf 1. Maar sinds de axiomatische invoering van de natuurlijke getallen door de 19e-eeuwse wiskundige Peano is het wel gemeengoed geworden om ook 0 tot de natuurlijke getallen te rekenen. Bovendien bij gebruik van de natuurlijke getallen als index is het handig om als laagste index 0 te nemen. In moderne programmeertalen is deze conventie bijna altijd overgenomen, soms onder directe verwijzing naar het manuscript EWD831 van de Nederlandse wiskundige en informaticus Edsger Wybe Dijkstra over dit onderwerp. Volgens de ISO 80000-2:2021 standaard over grootheden en eenheden behoort 0 tot de verzameling van natuurlijke getallen. De Bourbaki school in wiskunde gebruikt dezelfde conventie. Genoeg redenen om ook de regel te adopteren dat 0 een natuurlijk getal is.

Een veel gebruikte notatie bij bovenstaande keuze is: \(\mathbb{N}=\{0,1,2,3,\ldots\}\) en \(\mathbb{N}^\ast=\mathbb{N}_0=\{1,2,3,\ldots\}\). Met andere woorden: \(\mathbb{N}^\ast\) en \(\mathbb{N}_0\) symboliseren de verzameling van alle natuurlijke getallen zonder \(0\).

Gehele getallen Het rekenen met natuurlijke getallen gaat goed als je deze getallen bij elkaar optelt: in de context van tellen van objecten enkel een kwestie van doortellen. Maar het aftrekken van getallen geeft soms problemen. Wat is bijvoorbeeld de uitkomst van \(1-2\) of \(2-3\), en bedoelen we daar hetzelfde getal mee? Met andere woorden, wat is de oplossing van de vergelijking \(x+2=1\) of de vergelijking \(x+3=2\)? De wens om dergelijke vergelijkingen te kunnen oplossen geeft aanleiding tot de invoering van de verzameling van gehele getallen, aangeduid met \(\mathbb{ℤ}\).

Gehele getallen kun je op een getallenlijn uitzetten: begin met een eerste punt op een rechte lijn en geef dit het naamkaartje 0 en kies een tweede punt dat het naamkaartje 1 krijgt. We spreken af dat de afstand tussen deze twee punten gelijk is aan 1. Schrijd nu voort met passen van lengte 1 en zet steeds een volgend geheel getal als naamkaartje neer. Elk nummertje heeft een opvolger. Doe dit nu ook in de andere richting en geef elk nummertje een voorganger, en je krijgt de volgende getallenlijn:

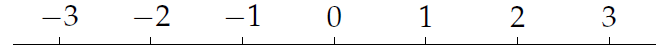
Dus \[\mathbb{ℤ}=\{\ldots, -2, -1, 0, 1, 2, \ldots\}\] De getallen uit deze verzameling kun je optellen, aftrekken en vermenigvuldigen met elkaar.

Tegengestelde Het tegengestelde van \(2\) is \(-2\) en andersom is \(2\) het tegengestelde van \(-2\). Kortom, \(2\) en \(-2\) zijn elkaars tegengestelde. Het getal \(0\) is zijn eigen tegengestelde.

We hebben dus drie soorten gehele getallen: het getal \(0\), de positieve natuurlijke getallen (getallen groter dan nul) en de negatieve gehele getallen (getallen kleiner dan nul). De negatieve gehele getallen hebben een minteken in hun notatie. Positieve getallen hebben als teken het plusteken, maar dat wordt gewoonlijk weggelaten (bijvoorbeeld: \({}+2=2\)).

Het tegengestelde van een willekeurig geheel getal \(n\) noteer je als \(-n\). Voor een positief getal spreekt dit voor zich. Maar ook als \(n\) negatief is, bedoelen we met \(-n\) het tegengestelde van \(n\), en dan is \(-n\) positief. Dus geldt bijvoorbeeld \(-(-2)=2\).

Het tegengestelde van een geheel getal krijg je dus als het teken ervan omklapt: \(-\) voor een cijfer wordt \(+\) en eventueel weggelaten, en andersom \(+\) (al dan niet expliciet voor het eerste cijfer opgeschreven) wordt \(-\).

Niet-positief en niet-negatief Een getal noemen we niet-positief als het negatief is of gelijk aan \(0\). Een getal noemen we niet-negatief als het positief is of gelijk aan \(0\).

Absolute waarde De absolute waarde \(|a|\) van een geheel getal \(a\) is gelijk aan \(a\) als het getal niet-negatief is, en aan \(-a\) als het getal negatief is. In formuletaal: voor elk geheel getal \(a\) geldt dat \[ |a|=\begin{cases} \phantom{-}a\quad\text{als }a\ge 0\\ -a\quad\text{als }a\lt 0\end{cases}\] Bijvoorbeeld: \(|-2|=2\) en \(|2|=2\).

Gehele getallen als pijlen langs de getallenlijn De gelabelde posities in de getallenlijn stellen de gehele getallen voor. Maar je kunt ook een pijl met beginpunt \(0\) en eindpunt in een gelabeld punt als voorstelling van een geheel getal beschouwen. Dan hoort een pijl naar rechts bij een natuurlijk getal groter dan \(0\) en hoort een pijl naar links bij een negatief getal. Hieronder zie je de pijlen horende bij de getallen \(-2\) en \(3\).

Deze voorstelling suggereert een beweging: zoveel stappen naar rechts of zoveel stappen naar links.

Optellen van twee getallen is in deze interpretatie van de getallenlijn dan het samenvoegen van de pijlen volgens de kop-staart methode. Hieronder zie je de optellingen \(2+1\) en \(1+2\) gevisualiseerd en het resultaat is hetzelfde, namelijk de pijlvoorstelling van het getal \(3\) op de getallenlijn. Immers, eerst twee stappen naar rechts gevolgd door één stap naar rechts levert dezelfde beweging van drie stappen naar rechts op als eerst één stap naar rechts gevolgd door twee stappen naar rechts.

Dit is een voorbeeld van een eigenschap van optelling van natuurlijke getallen: de uitkomst van een optelling van twee natuurlijke getallen verandert niet als je de twee getallen in de bewerking verwisselt. Dit heet de wisseleigenschap of, meer formeel, de commutatieve eigenschap van optellen van natuurlijke getallen.