Addition, subtraction, multiplication and exponentiation are called arithmetic calculations because they make new integers from given integers.
Division is also an arithmetic calculation with integers, but that does not always produce an integer. Only division with remainder, also referred to as Euclidean division, can always be applied successfully with this set of numbers.
Priority rules are used in arithmetic calculations with integers.
- addition and subtraction are carried out in the order in which these operations occur, from left to right.
- multiplication and exponentiation are carried out carried out in the order in which these operation occur, from left to right.
- exponentiation takes precedence over multiplication, and multiplication takes precedence over addition and subtraction.
Via parentheses you can change the default order of arithmetic calculations.
\[\begin{aligned}6-3+2&= (6-3)+2=5&\blue{\text{convention when no parentheses are placed}}\\ 6-(3+2)&= 1 & \\6-3\times 2&= 6-(3\times 2)=0&\blue{\text{convention when no parentheses are placed}}\\ (6-3)\times 2&= 6& \end{aligned}\]
When you add to a bin containing four marbles three times one marble, then you have hereafter a bin that contains seven marbles. You could also have placed first three marbles in your hand or in an extra bin, and then you could have merged the contents in order to get a bin with seven marbles. The following figure visualises the process of emptying of the container with three marbles into the container with four marbles.

You have in fact added the numbers \(4\) and \(3\), leading to the outcome \(7\). This is expressed in the equality \(4+3=7\). We pronounce it as "four plus three equals seven" when we want to focus on the calculation of the final outcome. In the statement "two plus three equals seven" we emphasize that these are equivalent representations of the number seven: this may be the number \(7\), and the outcome of the sum \(3+4\), but also the outcome of say \(2+5\). The terms on the left- and right-hand side are permitted nametags for one and the same mathematical object.
Via tabs below you get access to more details about addition of natural numbers and to a systematic approach toward addition of natural numbers.
When you have two bins with \(4\) and \(3\) marbles, respectively, and put all marbles into a single bin, then you have in the end \(7\) marbles. It does not matter whether you put three marbles from the one bin into the other bin with four marbles or, vice verse, put four marbles from the one bin into the other bin with three marbles. The result will always be a bin with seven marbles. In other words, \(4+3=3+4\) and the outcome \(7\) does not depend on the order of addition.
In general, the two numbers in an addition may be exchanged: this has no effect on the outcome of the calculation. In mathematical language: \[a+b=b+a\qquad\text{for arbitrary number }a\text{ and }b\tiny.\] This is called the commutative property or abelian property of addition of (natural) numbers, or less dignified the exchange property of addition of numbers.
If you want to indicate the precise order in which calculations should take place, then you must use parentheses. For example, \(3 + (2+1)\) means: first add \(2\) and \(1\) (intermediate result \(3\)), and then add this intermediate result to \(3\) yielding \(6\) as the final outcome. By the way, this result is also equal to the outcome of adding the number in the default order from left to right [first adding \(3\) and \(2\) (intermediate result \(5\)), and then adding \(1\)]. In other words \((3+2)+1=3 + (2+1)\).
In general, for any three (natural) numbers \(a\), \(b\), and \(c\) we have: \[(a+b)+c=a+(b+c)\] This is called the associative property of addition of numbers, or less dignified the chain property of addition of numbers.
Both properties of addition, namely commutativity and associativity, together imply that the order in which you add (natural) numbers does not matter to the final outcome.
With marbles in bins one can illustrate various additions. For example \(0+4=4\):

In general it is true that zero plus some number is always equal to the number that you add. In mathematical language: \[0+a=a\qquad\text{for any number }a\text.\]
When you know that \(4+3=7\) and how this can be visualised with marbles in bins, then you can also do that for adding tens such as \(40+30\). In the figure below you see that four columns of ten marbles in the bin on the left and three columns of ten marbles in the middle bin, when put together in one bin leads the bin on the right with seven columns of ten marbles.
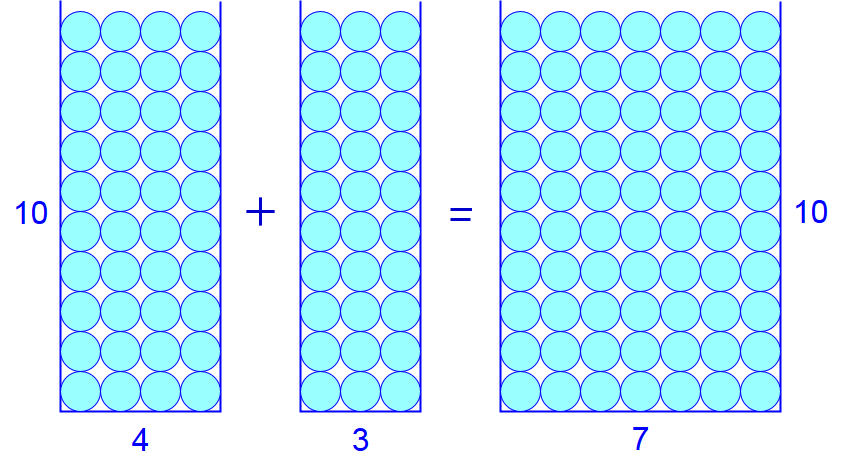
Four tens plus three tens add up to seven tens. So you can add tens simply by ignoring the trailing zeros and in the end by putting a zero behind. After all, when you put a zero behind a number, then you make it ten times greater.
Adding hundreds and thousands can be done in similar ways.
Four hundred plus three hundred add up to seven hundreds, that is \(400+300=700\). So you can add hundreds by simply ignoring the last two zeros and in the end by putting two zeros behind. After all, when you put two zeros behind a number, then you make it hundred times greater.
Four thousand plus three thousands add up to seven thousands, that is \(4000+3000=7000\). So you can add thousands by simply ignoring the last three zeros and in the end by putting three zeros behind. After all, when you put three zeros behind a number, then you make it thousand times greater.
In the following visualisation of addition we keep the marbles, but remove the bins. We also separate the columns of ten marbles a bit from the column with less than ten marbles by extra white space.
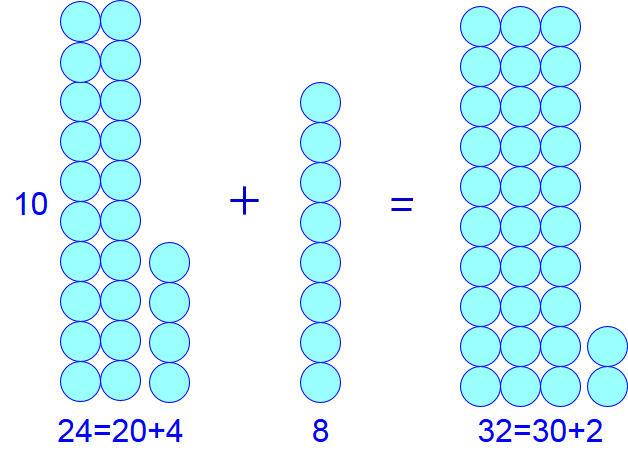
When you want to calculate \(24+8\), you split your \(24\) into \(20\) plus \(4\). Because \(4+8=12\), you have then \(24+8=20+4+8=20+12=20+10+2=30+2\).
The following figure represents this addition.
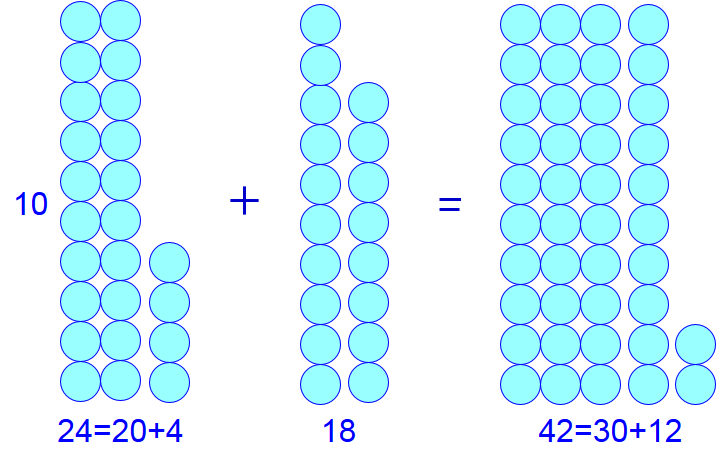
We consider how can add two numbers consisting of two digits. We take the example \(24+18\). It goes in several small steps:
- First, calculate with the units \(4+8=12\) and split the result in this case into \(12=10+2\).
- Add the tens \(20+10=30\)
- Now add the intermediate results and get the final outcome: \(30+12=30+10+2=42\)
This process is visualised below.
Addition of natural numbers by pencil and paper is most systematically carried out by aligning the number to the right and then by calculating columnwise. The above addition follows the recipe below:
- Place the numbers underneath each other and right-aligned \[\begin{array}[t]{rl} 24 & \\ 18 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +}\end{array}\]
- Add the units (the numbers in the column on the right): \(4+8=12\) and from this number you only write \(2\) at the bottom line and you move the \(1\) to the top of the next column (i.e., the columns of tens).
- Add the tens, i.e. add the first digits of the two-digit numbers, and add the additional \(1\): \(1+2+1=4\).
The following scheme illustrates the steps in the calculation, wherein we remove the extra digit at the top in the final stage. \[\begin{aligned}
&\textit{units:}\qquad \\ \begin{array}[t]{rl} & \\ 2\blue{4} & \\ 1\blue{8} \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ \color{royalblue}{1}\blue{2} & \end{array}
\quad &\longrightarrow\qquad \begin{array}[t]{rl} 1\phantom{2} & \\ 24 & \\ 18 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ 2 & \end{array} \\ \\
&\textit{tens:}\qquad \\
\begin{array}[t]{rl} \blue{1}\phantom{2} & \\ \blue{2}4 & \\ \blue{1}8 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ \blue{4}2 & \end{array}
\quad &\longrightarrow\qquad \begin{array}[t]{rl} & \\ 24 & \\ 18 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ 42 & \end{array}
\end{aligned}\] Experienced persons do not write down the numbers that we have placed at the top of the columns, but they memorise them and take them into account in further arithmetic calculations. They get:
\[\begin{aligned} 4+8=12,\quad &\blue{2\text{ written, }1\text{ memorised.}} \\ \blue{1}+2+1=4\phantom{2,} \quad &\blue{\text{ready; outcome}=42.}\end{aligned}\] Transcribed into two steps, with head calculations and memorising the additional ten: \[\begin{array}[t]{r}\blue{\textit{step 1:}} \\ \\ \\ \end{array}\quad \begin{array}[t]{rl} 24 & \\ 18 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ \phantom{4}2 & \end{array} \qquad \begin{array}[t]{r}\blue{\textit{step 2:}} \\ \\ \\ \end{array}\quad \begin{array}[t]{rl} 24 & \\ 18 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ 42 & \end{array}\]
When you remove three times one marble from a bin with seven marbles and put it in a second bin, then you have afterwards a second bin with three marbles and only four marbles are left in the original bin. The figure below visualises the process of removing three marbles from a bin with seven marbles and the placement of three marbles in an initially empty second bin (the white circles in the middle bin only indicate how many marbles will be transferred into it).
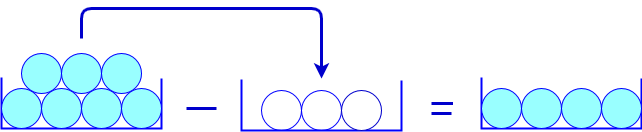
You have basically subtracted the number \(3\) from \(7\). This you indicate by the equality \(7-3=4\) and you pronounce it as "seven minus three gives four" or "seven minus three equals four," depending on whether you focus more on the operation or on the number four.
The subtraction \(3-7\) is not possible within the set of natural numbers because \(3\) is less than \(7\). This subtraction only makes sense within the set of integers and then the result is the negative number \(-4\). What you actually first do is swapping the two numbers in the subtraction: you get a subtraction that can be resolved within the set of natural numbers. Hereafter you take the opposite of the intermediate result.
With marbles in bins one can illustrate various subtractions. For example \(4-0=4\), wherein the middle bin in the figure remains empty:

In general it is true that some number minus zero is always equal to the initial number. In mathematical language: \[a-0=a\qquad\text{for any number }a\text.\]
When you know that \(7-3=4\) and how this can be visualised with marbles in bins, then you can also do that for subtracting tens such as \(70-30\). The figure below visualises the process of removing three columns of ten marbles from a bin with seven columns of ten marbles and the addition of these three columns of ten marbles to an initially empty second bin (the white circles in the middle bin only indicate how many marbles will be transferred into it). Four columns of ten marbles are left in the original bin.
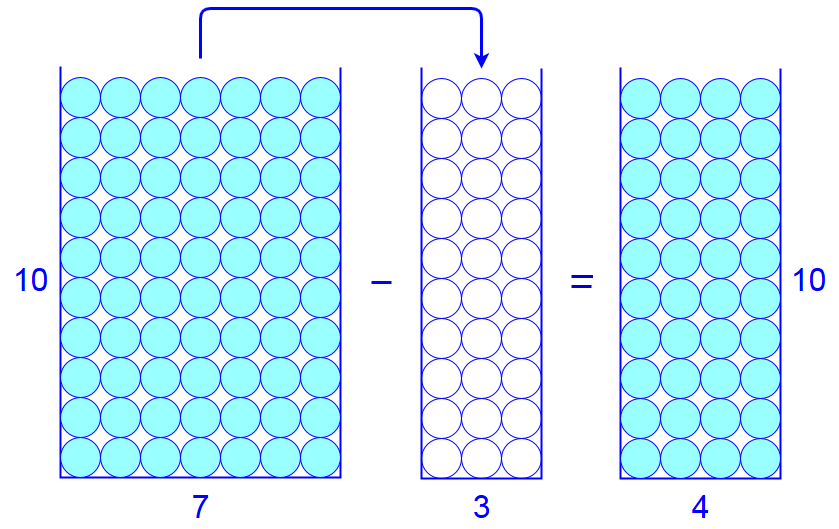
Seven tens minus three tens equals four tens. So you can subtract tens simply by ignoring the trailing zeros and in the end by putting a zero behind. After all, when you put a zero behind a number, then you make it ten times greater.
Subtracting hundreds and thousands can done in similar ways.
Seven hundreds minus three hundreds is equal to four hundreds, that is \(700+300=400\). So you can subtract hundreds by simply ignoring the last two zeros and in the end by putting two zeros behind. After all, when you put two zeros behind a number, then you make it hundred times greater.
In the following visualisation of subtraction we keep the marbles, but remove the bins. We also separate the columns of ten marbles a bit from the column with less than ten marbles by extra white space.
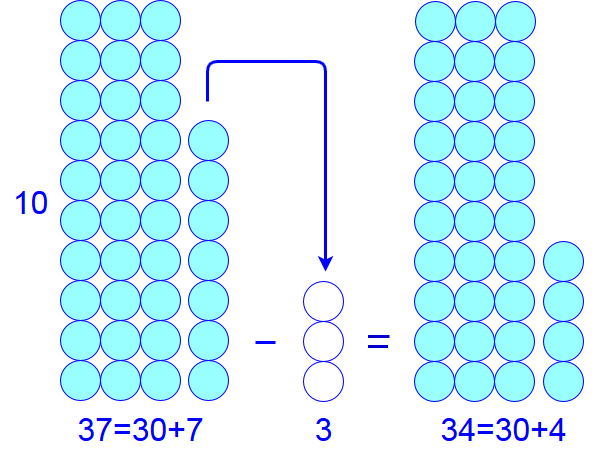
When you want to calculate \(37-8\), you split your \(37\) into \(30\) plus \(7\). Because \(7-3=4\), you have then \(37-3=30+7-3=30+4=34\). In fact, you pull the calculation with the units apart.
The following figure corresponds with this subtraction.
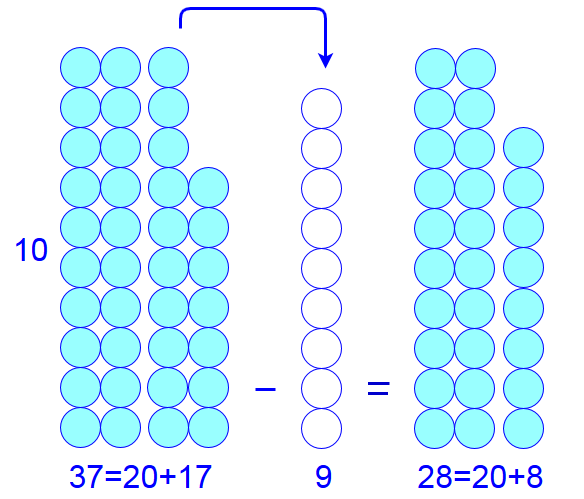
But what can you do when the subtraction is \(37-9\)? Now you can not subtract the units because \(7\) is less than \(9\). Splitting of \(37\) into \(20+17\) helps. Because the second amount of marbles is small you can easily calculate \(17-9\). You just take \(9\) marbles from the pile of \(17\) marbles and have \(8\) left. Obviously you should be able to do such subtraction in your head. This approach means that you borrow a ten of the three tens and leave the other two columns intact. In the figure below this is visualised.
Subtraction of natural numbers by pencil and paper is most systematically carried out by aligning the numbers to the right and then by calculating columnwise. The subtraction \(37-19\) follows the recipe below:
- Place the numbers underneath each other and right-aligned \[\begin{array}[t]{rl} 37 & \\ 19 & \\ \overline{\phantom{xx}}& {}^{\displaystyle -}\end{array}\]
- Subtract the units (the digits in the column to the right) goes immediately wrong because \(7\) is less than \(9\). The solution is to 'borrow' a \(1\) from the digit indicating the tens and to subtract \(1\) from that digit. You get \(17-9=8\) as unit in the intermediate result.
- Subtract the (modified) tens: \(2-1=1\) is the number of tens in the final result and together with the previously calculated unit you have systematically calculated the result of the subtraction.
The following scheme illustrates the steps in the calculation, in which we represent the borrowing of a 1 and its consequences too.
Units \[\begin{array}[t]{rl} \blue{2}\phantom{7}\\ \blue{3 {\kern -5pt /}}7 & \\ 19 & \\ \overline{\phantom{xxxxxx}}& {}^{\displaystyle -} \\ 8 & \end{array}\] Tens: \[\begin{array}[t]{rl} \blue{2}\phantom{7}\\ 3 {\kern -5pt /}7 & \\ \blue{1}9 & \\ \overline{\phantom{xxxxxx}}& {}^{\displaystyle -} \\ \blue{1}8 & \end{array}\] So: \(27-19=8\).
\(\phantom{x}\)
We discuss a second example, the subtraction \(307-119\) in which the digit from which you have to borrow is \(0\). Then you just borrow a \(1\) further to the left. In this example, you borrow from \(30\) and change \(30\) in \(29\). The scheme below describes the steps in this subtraction.
Units \[\begin{array}[t]{rl} \blue{29}\phantom{7}\\\blue{3 {\kern -5pt /} 0 {\kern -5pt /}}7 & \\ 119 & \\ \overline{\phantom{xxxxxx}}& {}^{\displaystyle -} \\ 8 & \end{array}\] Tens: \[\begin{array}[t]{rl} \blue{29}\phantom{7}\\3 {\kern -5pt /} 0 {\kern -5pt /}7 & \\ 1\blue{1}9 & \\ \overline{\phantom{xxxxxx}}& {}^{\displaystyle -} \\ \blue{8}8 & \end{array}\] Hundreds: \[\begin{array}[t]{rl} \blue{29}\phantom{7}\\3 {\kern -5pt /} 0 {\kern -5pt /}7 & \\ \blue{1}19 & \\ \overline{\phantom{xxxxxx}}& {}^{\displaystyle -} \\ \blue{1}88 & \end{array}\] So: \(307-119=188\).
When you put three columns of four marbles together, you have built a structure with a total of \(3\times 4=12\) marbles.
This illustrates that multiplication of natural numbers not more or less than repeated addition: in our example: \(3\times 4=4+4+4=12\).
We pronounce \(3\times 4=12\) as "three times four is twelve" or "three times for makes twelve" when we want to focus more on the calculation of the final result. Through he statement "three times four equals twelve" we emphasize that these are equivalent representations of the number 12: This may be the number \(12\) or the result of the calculation \(3\times 4\), but also the outcome of for example \(2\times 6\) or \(1\times 12\). The terms on the left and right are valid nametags for the same mathematical object.
When you put three columns of four marbles next to together, you have a structure built with a total \(3\times 4=12\) marbles. Conversely, when you have four columns of three marbles put together, then you have built a structure with a total of \(4\times 3=12\) marbles. In other words, \(4\times 3=3\times4\) and the outcome is always equal to \(12\), regardless of the order of multiplication.
In general, two (natural) numbers in a multiplication may be swapped: this has no effect on the outcome of the calculation. In mathematical language: \[a\times b=b\times a\qquad\text{for any numbers }a\text{ and }b\tiny.\] This is called the commutative property or abelian property of multiplication of numbers, or less dignified the exchange property of multiplication.
If you want to indicate the precise order in which calculations should take place, then you must use parentheses. For example, \(4 \times (3\times 2)\) means, first multiply \(3\) and \(2\) (intermediate result \(6\)), and then multiply this intermediate result by \(4\), leading to the final outcome \(24\). This outcome is also equal to that of the multiplication in the usual order from left to right [First multiply \(4\) and \(3\) (intermediate result \(12\)), and then multiply by \(2\)]. In other words \((4\times 3)\times 2=4 \times (3\times 2)\).
In general, for any three numbers \(a\), \(b\) and \(c\): \[(a\times b)\times c=a\times (b\times c)\] This is called the associative property of multiplication of numbers, or less dignified, the exchange property of multiplication of numbers.
Both properties of addition, namely commutativity and associativity, together imply that the order in which you multiply (natural) numbers does not matter to the final outcome.
Because multiplication of natural numbers is actually repeated addition, for example, we have for example \(4\times 0=0+0+0+0=0\).
In general, if you have a certain number of zero, multiply the result is always zero. In formula language: \[a\times 0=0\qquad\text{for any number }a\tiny.\]
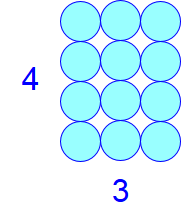
The distributive property is the property that one distributes the numbers in a calculation, for example for reasons of convenience. Two simple examples with an addition and subtraction, respectively, and a multiplication: \[3\times (10+4)=3\times 10+3\times 4\quad\text{and}\quad 3\times (10-4)=3\times 10-3\times 4\tiny.\] With other natural numbers it just goes the same. For example, \((2+3)\times 4=2\times 4 + 3\times 4\). The left-hand side can be thought of as the area of a rectangle with length \(2+3=5\) and width \(4\). The area of this rectangle is equal to the sum of the areas of the two rectangles of smaller size in the figure below, with dimensions of \(2\times 4\) and \(3\times4\), respectively.
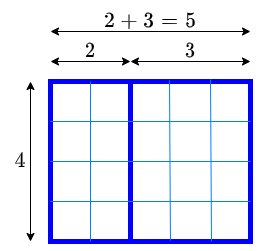
So for any three natural numbers, say denoted by the letters \(a\), \(b\) and \(c\), we have in mathematical language: \[a\times (b+c)=a\times b + a\times c\quad\text{and}\quad a\times (b-c)=a\times b - a\times c\tiny.\] We also say that the parentheses have been expanded. To make it easier to recall, you may add arcs above or below, for example:
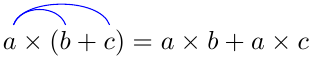
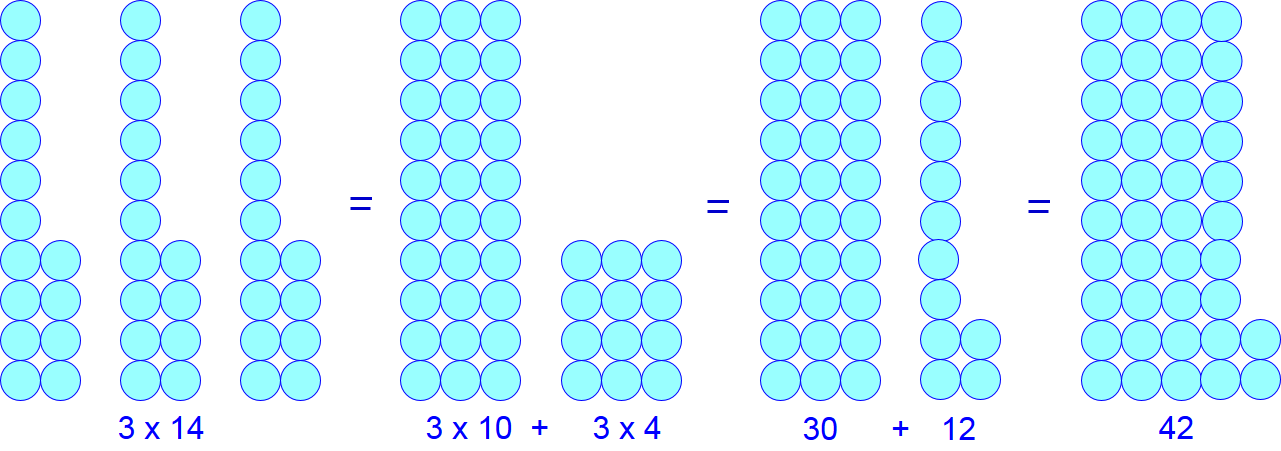
With the distributive property you can carry out somewhat more difficult multiplication calculations and visualise the process: \[\begin{aligned}3\times 14&=3\times(10+4)&\phantom{abcxyz} \blue{\text{splitting of tens and units}}\\ &=3\times 10+3\times 4&\phantom{abcxyz} \blue{\text{applying the distributive property}}\\ &=30+12&\phantom{abcxyz} \blue{\text{multiplying small numbers}}\\ &=42&\phantom{abcxyz} \blue{\text{adding natural numbers}}\end{aligned}\]
Because the letter \(x\) and the symbol \({}\times{}\) for multiplication look very similar to each other, one often alternatively uses \({}\cdot{}\) (in software environments or calculators often \({}*{}\) ). As long as none of confusion may arise, one even omits the multiplication symbol in formulas with letters at the end. So instead of \(2\times k\) or \(2\cdot k\) one writes in short \(2k\). Properties of multiplication are then written as \[ab=ba,\qquad (ab)c=a(bc), \qquad a(b+c)=ab+ac,\qquad\text{for any numbers }a, b\text{ and }c\tiny.\]
Multiplication of natural numbers by pencil and paper is most systematically carried out by aligning the numbers to the right and then by calculating columnwise. The multiplication \(3\times 654\) follows the recipe below:
- Place the numbers underneath each other and right-aligned \[\begin{array}[t]{rl} 654 & \\ 3 & \\ \overline{\phantom{xx}}& {}^{\displaystyle \times}\end{array}\]
- Multiply the units (the digits in the column to the right): \(3\times 4=12\).
- Multiply the tens in the top number (digit in the middle column): \(3\times 50=150\).
- Multiply the hundreds in the top number (digit in the left column): \(3\times 600=1500\).
- Add the intermediate results and you get the result of the multiplication in a systematic way: \(3\times 654=1500+150+12=1962\).
You can also do all steps at once: \[\begin{array}[t]{rl} 654 & \\ 3 & \\ \overline{\phantom{xxx}}& {}^{\displaystyle \times}\\ 2 & \end{array} \qquad \qquad\begin{array}[t]{rl} 654 & \\ 3 & \\ \overline{\phantom{xxx}}& {}^{\displaystyle \times}\\ 62 & \end{array} \qquad\qquad \begin{array}[t]{rl} 654 & \\ 3 & \\ \overline{\phantom{xxx}}& {}^{\displaystyle \times}\\ 1962 & \end{array} \] Notes: \[\begin{aligned} 3\times 4=12,\quad &\blue{2\text{ written, }1\text{ memorised.}} \\ \blue{1}+3\times 5=16, \quad &\blue{6\text{ written, }1\text{ memorised.}} \\ \blue{1}+3\times 6=19.\quad &\blue{\text{ready; outcome}=1962.}\end{aligned}\]
In this way you can always succeed in multiplying a number by a one digit number.
The multiplication \(30\times 654\) can be carried out in a similar way by actually calculating \(3\times 654=1962\) and add a zero at the end of this intermediate result.
The multiplication \(23\times 654\) can be carried out in two steps: \(3\times 654=1962\) and \(20\times 654=13080\). Next, add the intermediate results: \(1962+13080=15042\).
In summary: \[\begin{array}[t]{rlcr} 654 & & & \\ 23 & & & \\ \overline{\phantom{xxx}}& {}^{\displaystyle \times} & & \\ 1962 & & \blue{\leftarrow} & \blue{3\times 654}\\ 13080 & & \blue{\leftarrow} & \blue{20\times 654}\\ \overline{\phantom{xxx}}& {}^{\displaystyle +} & & \overline{\phantom{xxxxxxxx}}& \\ 15042 & & \blue{\leftarrow} & \blue{23\times 654}\end{array}\]
A final example shows how the multiplication of numbers with more than two digits can be organized similarly. For all intermediate results we indicate on the right-hand side how they are calculated, but in practice you do not have to write this down in a calculation. Then you work only with what is on the left-hand side, but you do mind the placement of the trailing zeros created in blue. \[\begin{array}[t]{rlcr} 654 & & & \\ 123 & & & \\ \overline{\phantom{xxx}}& {}^{\displaystyle \times} & & \\ 1962 & & \blue{\leftarrow} & \blue{3\times 654}\\ 1308\color{blue}{0} & & \blue{\leftarrow} & \blue{2\color{blue}{0}\times 654}\\ 654\color{blue}{00} & & \blue{\leftarrow} & \blue{1\color{blue}{00}\times 654}\\ \overline{\phantom{,xxxx}}& {}^{\displaystyle +} & & \overline{\phantom{xxxxxxx}}& \\ 80442 & & \blue{\leftarrow} & \blue{123\times 654}\end{array}\]
\(\phantom{x}\)
Addition, subtraction, and multiplication of natural numbers is most systematically done by placing the numbers underneath each other and aligned to the right aligned at each place and by calculating columnwise. If needed, look at a few examples and study the additional information below the tabs in the above frames.
Carry out the following calculation:
\[\begin{array}[t]{rl} 263 & \\ 96 & \\ 956 & \\ 96 & \\ 187 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +}\end{array}\]
The correct answer is \(1598\).
You learned in elementary school to add such numbers, but perhaps not in the most convenient and systematic way. The best recipe is as follows:
- Place the numbers right-aligned below each other
- Add the units (digit in the right column): \(3+6+6+6+7=28\), and write of this number only \(8\) on the bottom line and move \(2\) to the top of the next column (the tens).
- Add the tens, i.e. add the middle digits of a three-digit number, together with the additional \(2\): \(2+6+9+5+9+8=39\). Again you write \(9\) on the bottom line and move \(3\) to the top of the next column on the left.
- Add the hundreds together with the extra \(3\): \(3+2+9+1=15\). The outcome at the bottom line and you're done with the calculation of the outcome \(1598\).
The following diagram illustrates the steps in the calculation; we remove at the end the extra digits added on the top.
\[\begin{aligned}
&\textit{units:}\qquad \\ \begin{array}[t]{rl} & \\ 26\blue{3} & \\ 9\blue{6} & \\ 95\blue{6} & \\ 9\blue{6} & \\ 18\blue{7} & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ \blue2\blue{8} & \end{array} \quad &\longrightarrow\qquad \begin{array}[t]{rl} \phantom{2}2\phantom{3} & \\ 263 & \\ 96 & \\ 956 & \\ 96 & \\ 187 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ 8 & \end{array}
\\ \\
&\textit{tens:}\qquad \\
\begin{array}[t]{rl} \phantom{2}\blue{2}\phantom{3} & \\ 2\blue{6}3 & \\ \blue{9}6 & \\ 9\blue{5}6 & \\ \blue{9}6 & \\ 1\blue{8}7 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ \blue3\blue{9}8 & \end{array} \quad &\longrightarrow\qquad \begin{array}[t]{rl} 32\phantom{3} & \\ 263 & \\ 96 & \\ 956 & \\ 96 & \\ 187 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ 98 & \end{array}
\\ \\
&\textit{hundreds:}\qquad \\
\begin{array}[t]{rl} \blue{3}2\phantom{3} & \\ \blue{2}63 & \\ 96 & \\ \blue{9}56 & \\ 96 & \\ \blue{1}87 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ \blue{15}98 & \end{array} \quad &\longrightarrow\qquad \begin{array}[t]{rl} \phantom{3} & \\ 263 & \\ 96 & \\ 956 & \\ 96 & \\ 187 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ 1598 & \end{array}
\end{aligned}\]
Experienced persons do not write the additional numbers at the top of the columns anymore, but they memorise then and add them immediately in their brains. They write:
\[\begin{aligned} 3+6+6+6+7=28,\quad &\blue{8\text{ written, }2\text{ memorised.}} \\ \blue{2}+6+9+5+9+8=39, \quad &\blue{9\text{ written, }3\text{ memorised.}} \\ \blue{3}+2+9+1=15.\quad &\blue{\text{ready; outcome}=1598.}\end{aligned}\]
\(\phantom{x}\)
So far we have focused on addition, subtraction, and multiplication of natural numbers. This forms the basis for calculating with integers (which may be negative).
Subtraction within the set of integers is rather easy when you apply the following rule:
Subtraction of a number is exactly the same as adding the opposite number.
For example: \(1-3=1+(-3)=-2\).
The result is easily understood by representing the numbers as arrows along the number line and by combining them via the head-tail method.

Multiplication within the set of integers is rather easy when you apply the following rule:
Multiplying by \(-1\) is the same as the toggling of the sign, from plus to minus or from minus to plus.
Examples: \(3\times (-3)=3\times 3\times (-1)=9\times (-1)=-9\) and \((-3)\times (-4)=3\times (-1)\times 4\times (-1)=3\times 4\times (-1)\times (-1)=12\times (1)=12\).
Summarized in words and easy to recall: \[\begin{array}{ll} \textit{plus times plus is plus} & \textit{min times plus is min} \\ \textit{plus times min is min} & \textit{min times min is plus}\end{array}\]
 Arithmetic calculations with integers
Arithmetic calculations with integers
![]()


![]()










