Division with remainder

Calculating with numbers: Computing with integers

Division with remainder

When you fairly share $24$ marbles amongst $6$ children, you give share each child $4$ marbles and you get rid of all marbles; after all, $6\times 4=24$ . To calculate how many marbles you can give to each child you divide $24$ by $6$ ; in arithmetic language you write on $24:6=4$ and pronounce it as "twenty-six divided by six equals four".

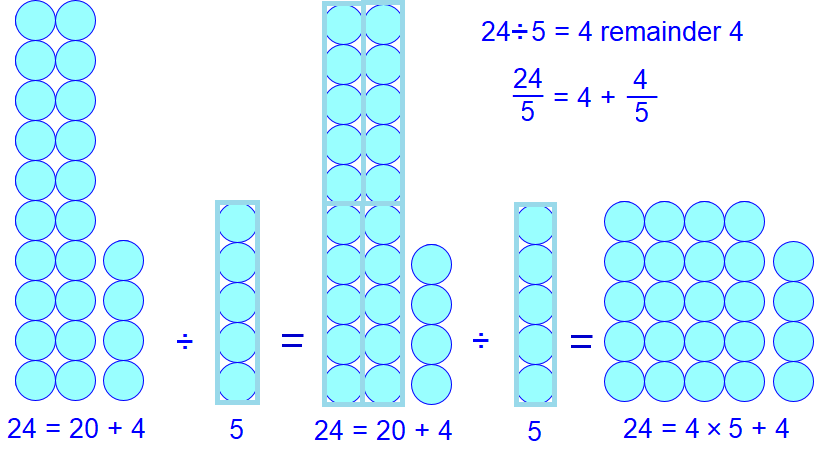
The division of $24$ by $6$ is usually denoted by $24:6$ , but other writings are $24/6$ and $24\div 6$ . Of course, the fractional notation $\displaystyle \frac{24}{6}$ is also widely used.

But can you do if you want to fairly share $24$ marbles amongst $5$ children? Even in this case you can start with giving each child $4$ marbles. Then you have already shared $5\times 4=20$ marbles, but there are still $4$ marbles left in your hands. If these remaining marbles are not given away through a lottery, you are left with the remaining marbles. In arithmetic language you write $24:5=4\textit{ remainder }4$ and pronounce it js "twenty divided by five equals four with a remainder of four."

This process of division in which a nonzero remainder is possible is called division with remainder or Euclidean division. In this example we call

the number of marbles the dividend;
the number of children who get the marbles divisor;
the number of marbles that every child gets the quotient;
the remaining number of marbles is the remainder.

We visualise $24\div 5=4\textit{ remainder }4$ as below, where we check how many times the number $5$ fits in $24$ . This can be done 4 times and there remain 4 marbles. This also means that the fraction $\frac{24}{5}$ can be written as $4$ plus $\frac{4}{5}$ . In mixed notation of fractions this is equal to $4\tfrac{4}{5}$ .

The following theorem makes mathematically more precise what we mean by division with remainder.

If $a$ and $b$ are natural numbers and $b>0$ , then there are unique natural numbers $q$ and $r$ such that $a=q \times b+r\qquad\text{and}\qquad 0\le r<b\text.$ We call $q$ the quotient and $r$ the remainder of the division with remainder of $a$ by $b$ .

The number $a$ is called divisible by $b$ when the remainder is equal to zero. In this case, we say that "the division terminates" and that " $b$ is a divisor of $a$ ".

The division $61 : 7$ has not a natural number as outcome. Calculate the quotient and the remainder after division.

$61 : 7 = 8 \textit{ remainder } 5$ After all $61 =8\times 7+5= 56+5$ This also means that the division within the set of rational numbers is as follows: $61 : 7 = 8\tfrac{5}{7}$

New example

Long division is the fastest and most systematic approach to pencil-and-paper calculations of the outcome of a division or a division with remainder. The example below illustrates this.

$\begin{array}[t]{rrl} 36\; \Bigm/ \!\!\! & 81218 & \!\!\! \Bigm{\backslash} \; 2256 \\ & \underline{72}\phantom{000} & \qquad \blue{\uparrow}\\ & \phantom{0}92\phantom{00} & \blue{\text{quotient}}\\ & \phantom{0} \underline{72}\phantom{00} & \\ & \phantom{0}201\phantom{0} & \\ & \phantom{0}\underline{180}\phantom{0} & \\ & \phantom{00}218 & \\ & \phantom{00}\underline{216} & \\ & \phantom{0000}2 & \blue{ \leftarrow \text{remainder}} \end{array}$ So: $81218= 2256\times 36 +2 \qquad\text{and}\qquad 81218:36 = 2256\textit{ remainder }2$ This implies the following exact calculation of the divsion: $81218:36 =2256\,\tfrac{2}{36}=2256\,\tfrac{1}{18}$

Instructional videos in Dutch from Stichting Goed Rekenonderwijs