Basisregels

Rekenen met letters: Rekenen met letters

Basisregels

Bij rekenen met getallen gelden prioriteitsregels.

Prioriteitsregels

Optellen en aftrekken geschieden in de volgorde waarin deze bewerkingen voorkomen, van links naar rechts.
Vermenigvuldigen en delen geschieden in de volgorde waarin deze bewerkingen voorkomen, van links naar rechts.
Vermenigvuldigen en delen hebben voorrang boven optellen en aftrekken.
Machtsverheffen heeft voorrang op vermenigvuldigen en delen.

"Meneer Van Dalen Wacht Op Antwoord" is een ezelbruggetje om de voorrangsregels voor het rekenen te onthouden: eerst Machten, dan Vermenigvuldigen, daarna Delen, vervolgens Worteltrekken, dan Optellen en tenslotte Aftrekken.

Met haakjes kun je de gewone volgorde wijzigen.

$\begin{aligned}6-3+2&= (6-3)+2=5\\ 6-(3+2)&= 1\\6-3\times 2&= 6-(3\times 2)=0\\ (6-3)\times 2&= 6\\ 6\div 3\times 2 &= (6\div 3)\times 2=4\\ 6\div(3\times 2&= 13-2 \end{aligned}$

Als je nu de getallen in een rekenkundige uitdrukking vervangt door letters krijg je een algebraïsche uitdrukking. De letters zijn dan als het ware reserveringsplekken voor getallen. Maar het kunnen ook symbolen voor een variabele grootheid zijn, bijvoorbeeld de letter $T$ voor temperatuur of $t$ voor tijd. We noemen zo'n letter een variabele.

Dezelfde prioriteitsregels als boven worden gehanteerd bij algebra, d.w.z. bij het rekenen met variabelen. Als je immers getallen invult voor de variabelen, moet je het resultaat van substitutie net zo kunnen interpreteren als bij rekenen met getallen. Je kunt dus ook met variabelen rekenen en bijvoorbeeld $x+y$ de som van $x$ en $y$ noemen of $2x$ de verdubbeling van $x$ noemen.

Maar je moet ook een beetje opletten wat je doet bij substitutie van getallen en bijvoorbeeld niet simpelweg $x$ in $2x$ vervangen door $4$ : substitutie van $x=4$ in $2x$ is namelijk niet gelijk aan $24$ , maar levert het getal $8$ op. De uitdrukking $2x$ staat immers voor $2\cdot x$ en bij substitutie krijg je in dit voorbeeld dus $2\cdot 4$ , met als eindresultaat $8$ . Let bij substitutie van negatieve getallen er op dat je zo nodig haakjes plaatst: substitutie van $x=-3$ in $x^2$ is namelijk niet gelijk aan $-3^2$ , maar $(-3)^2$ .

Substitueer

$x=4$ in de algebraïsche uitdrukking

$(3{x}-4)^2$ en bereken het resultaat.

Invullen van

$x=4$ in de uitdrukking

$(3{x}-4)^2$ geeft

$(3\times(4)-4)^2$ en doorrekenen leidt tot het resultaat

$64$

Nieuw voorbeeld

De volgende afspraken over notatie worden bij het rekenen met variabelen gehanteerd.

Afspraken over notatie en terminologie

Omdat het vermenigvuldigingsteken $\times$ te veel lijkt op de letter $x$ wordt het in formules vaak vervangen door een punt $x\cdot y$ of helemaal weggelaten $xy$ , als er geen verwarring mogelijk is.
In mengvormen van getallen en variabelen, bijvoorbeeld $2xy^3$ , is het gebruikelijk om de coëfficiënt voorop te zetten: dus $2xy^3$ en niet $x2y^3$ .
Als de notatie ruimte laat voor verschillende interpretaties of gewoonweg lastig te lezen is, dan gebruikt men vaak haakjes en de punt als maalteken: $2xy^3$ is volgens afspraak $2\cdot x\cdot\ y^3$ en is ongelijk aan $2(xy)^3$ of $(2xy)^3$ .

We bekijken enkele basisvormen van algebraïsche uitdrukkingen

Som en product

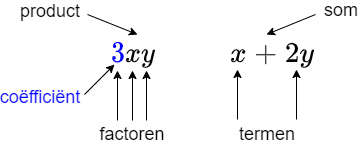
De uitdrukking $2xy$ is een product en het getal $2$ noemen we ook wel de coëfficiënt van $xy$ .

De uitdrukking $x+2y$ is een som met de termen $x$ en $2y$ . Het getal $2$ is de coëfficiënt van de term $2y$ .

Machten met gehele exponenten

Voor elke variabele $x$ en elk positief geheel getal $k$ is

$\begin{aligned} x^k&=\blue{ \overbrace{\color{black}{x \times x \times \cdots \times x}}^{k\mathrm{\;maal}}} \\ x^0\; & = 1 \\ x^{-k}\; & = \frac{1}{x^k} \end{aligned}$

Hiermee is $x^n$ voor elk geheel getal $n$ bepaald. Het getal $n$ heet de exponent. In plaats van $x^1$ schrijven we $x$ en we spreken af dat $x^0=1$ .

Voorbeelden

$\begin{aligned}(2x)^3 &= 8x^3\\[0.2cm] x^{-1}&=\frac{1}{x}\\[0.2cm] \frac{1}{2}x^{-3} &=\frac{1}{2x^3}\end{aligned}$

Machten met breuken als exponenten

Voor elke variabele $x$ en alle positief gehele getallen $m$ en $n$ is

$\sqrt[n]{x^m} =x^{\frac{m}{n}}$

Hiermee is $x^r$ voor elk positief rationaal getal $r$ bepaald. Het getal $r$ heet de exponent. We definiëren dan

$x^{-r}=\frac{1}{x^r}$ en hiermee is dan de macht met een willekeurige breuk als exponent vastgelegd. We noemen dergelijke uitdrukkingen ook wortels.

Voorbeelden

$\begin{aligned}\sqrt{x} &= x^{\frac{1}{2}}\\[0.2cm] \sqrt[5]{x^3}&=x^{\frac{3}{5}}\\[0.2cm] \frac{1}{\sqrt{x}} &=x^{-\frac{1}{2}}\\[0.2cm] \frac{1}{4}x^{-\frac{2}{3}} &=\frac{1}{4\sqrt[3]{x^2}}\end{aligned}$

Herleiden

De uitdrukking $2\cdot 3x$ kun je vereenvoudigen tot $6x$ . De uitdrukking $3x+4x-5x$ wordt overzichtelijker als je er $2x$ van maakt. Het eenvoudiger en overzichtelijker maken van een algebraïsche uitdrukking noemen we ook wel herleiden.

Bij het herleiden van uitdrukkingen gebruik je vaak de commutatieve associatieve en distributieve rekenregels om

berekeningen met getallen uit te voeren;
gelijksoortige termen, d.w.z. termen met dezelfde letters en exponenten, bij elkaar te nemen;
letters alfabetisch te ordenen en getallen voorop te zetten.

Voorbeelden

$\begin{aligned}2x+3+4x-5 &= 6x-2\\[0.2cm] y\cdot 2x\cdot 3y &= 6xy^2\\[0.2cm] \frac{xy^2}{2y}&=\tfrac{1}{2}xy\\[0.2cm] x^2 + 2x + 3x^2 + x^3 &=x^3+4x^2+2x\\[0.2cm] (2x+3x)4x &= 20x^2\\[0.2cm](-2xy^3)^4&=16x^4y^{12}\end{aligned}$

Herleid $-2b^2-2b^2$ .

$\begin{aligned}-2b^2-2b^2 &=(-2-2)\cdot b^2&\blue{\text{samenvoeging van coëfficienten}}\\ &=-4b^2&\blue{\text{berekening van eindresultaat}}\end{aligned}$

Nieuw voorbeeld

Mathcentre videos

Rules of Arithmetic (29:07)

$\phantom{x}$

Substitution in Formulae (20:58)

$\phantom{x}$

Mathematical Language (21:24)