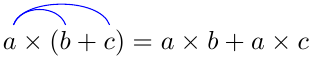Optellen, aftrekken, vermenigvuldigen en machtsverheffen heten rekenkundige bewerkingen omdat ze uit gehele getallen nieuwe gehele getallen maken.
Delen is ook een rekenkundige bewerking van gehele getallen, maar dat levert niet altijd een geheel getal op. Alleen delen met rest, ook wel Euclidische deling genoemd is binnen deze getallenverzameling te hanteren.
Bij rekenen met gehele getallen gelden voorrangsregels (ook wel prioriteitsregels genoemd)
- optellen en aftrekken geschieden in de volgorde waarin deze bewerkingen voorkomen, van links naar rechts.
- vermenigvuldigen en machtsverheffen geschieden in de volgorde waarin deze bewerkingen voorkomen, van links naar rechts.
- machtsverheffen heeft voorrang boven vermenigvuldigen, en op zijn beurt heeft vermenigvuldigen voorrang boven optellen en aftrekken.
Met haakjes kun je de gewone volgorde wijzigen.
\[\begin{aligned}6-3+2&= (6-3)+2=5&\blue{\text{conventie als er geen haakjes staan}}\\ 6-(3+2)&= 1 & \\6-3\times 2&= 6-(3\times 2)=0&\blue{\text{conventie als er geen haakjes staan}}\\ (6-3)\times 2&= 6& \end{aligned}\]
Als je in een bak met vier knikkers driemaal één knikker toevoegt, dan heb je na afloop een bak met zeven knikkers. Je had natuurlijk ook eerst drie knikkers in je hand of een extra bak kunnen stoppen, en daarna de inhoud bij elkaar kunnen voegen om zo een bak met zeven knikkers te krijgen. Onderstaand plaatje visualiseert het proces van het ledigen van de bak met drie knikkers in de bak met vier knikkers.

Je hebt in feite de getallen \(4\) en \(3\) opgeteld, met als uitkomst \(7\). Dit geef je aan met de gelijkheid \(4+3=7\). We spreken dit uit als "vier plus drie is zeven" wanneer we het accent willen leggen op het rekenwerk met het eindresultaat. Met de uitspraak "vier plus drie is gelijk aan zeven" benadrukken we dat het gaat om equivalente voorstellingen van het getal zeven: dit kan het cijfer \(7\) zijn en de uitkomst van de som \(3+4\), maar ook de uitkomst van bijvoorbeeld \(2+5\). De uitdrukkingen links en rechts zijn dan toegestane naamkaartjes voor hetzelfde wiskundige object.
Via onderstaande tabs krijg je toegang tot meer details over het optellen van natuurlijke getallen en wordt een systematische aanpak van optellen toegelicht.
Als je twee bakken met respectievelijk \(4\) en \(3\) knikkers hebt en alle knikkers in één bak bij elkaar gooit, dan heb je er \(7\). Het maakt hierbij niet uit of je de drie knikkers uit de ene bak toevoegt aan de bak met vier knikkers of andersom de vier knikkers uit de ene bak toevoegt aan de bak met drie knikkers. Het resultaat is altijd een bak met zeven knikkers. Met andere woorden: \(4+3=3+4\) en de uitkomst is ongeacht de volgorde van optellen gelijk aan \(7\).
In het algemeen geldt dat twee getallen in een optelling verwisseld mogen worden: dit heeft namelijk geen effect op de uitkomst van de bewerking. In formuletaal: \[a+b=b+a\qquad\text{voor willekeurige getallen }a\text{ en }b\tiny.\] Dit heet de commutatieve eigenschap van optellen van (natuurlijke) getallen, of wat minder deftig, de wisseleigenschap van optelling van getallen.
Als je bij berekeningen een precieze volgorde van bewerkingen wilt aangeven, dan moet je haakjes gebruiken. Bijvoorbeeld, \(3 + (2+1)\) betekent eerst \(2\) en \(1\) bij elkaar optellen (tussenresultaat \(3\)), en vervolgens dit tussenresultaat bij \(3\) optellen met \(6\) als einduitkomst. Deze uitkomst is overigens ook gelijk aan die van de optelling in de gebruikelijk volgorde van links naar rechts [eerst \(3\) en \(2\) bij elkaar optellen (tussenresultaat \(5\)), en vervolgens hierbij \(1\) optellen]. Met andere woorden: \((3+2)+1=3 + (2+1)\).
In het algemeen geldt voor drie willekeurige (natuurlijke) getallen \(a\), \(b\) en \(c\): \[(a+b)+c=a+(b+c)\] Dit heet de associatieve eigenschap van optellen van getallen, of wat minder deftig, de schakeleigenschap van optelling.
De beide eigenschappen betekenen samen dat de volgorde waarin je natuurlijke getallen optelt niet uitmaakt voor de einduitkomst.
Met knikkers in bakken kun je allerlei optellingen illustreren. Bijvoorbeeld \(0+4=4\):

In het algemeen geldt dat nul plus een zeker getal altijd gelijk is aan het getal dat je optelt. In formuletaal: \[0+a=a\qquad\text{voor een willekeurig getal }a\text.\]
Als je weet dat \(4+3=7\) en hoe dit gevisualiseerd kan worden met knikkers in bakken, dan kan dat ook doen voor optellen van tientallen zoals bijvoorbeeld \(40+30\). In onderstaande figuur zie je dat vier kolommen van tien knikkers in de bak links en drie kolommen van tien knikkers in de middelste bak bij samenvoeging een bak rechts opleveren met zeven kolommen van tien knikkers.
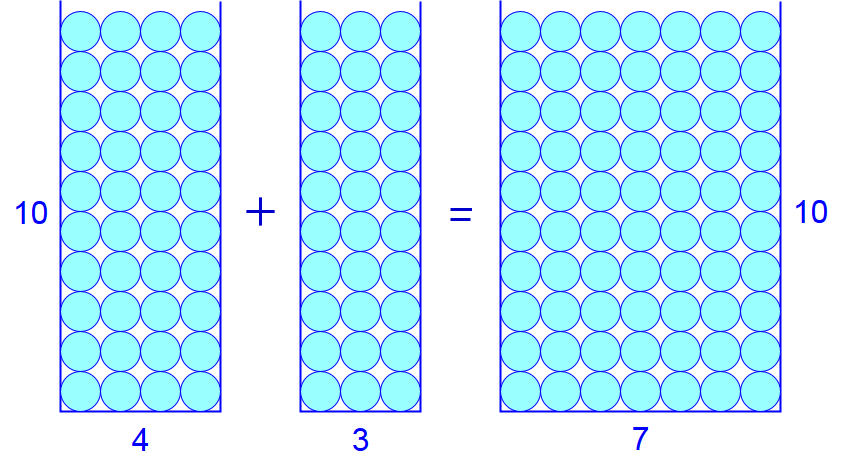
Vier tientallen plus drie tientallen is samen zeven tientallen. Je kunt tientallen dus optellen door gewoon zonder nullen op te tellen en er dan weer een nul achter te zetten. Immers, als je een nul achter een getal zet, dan maak je het tienmaal zo groot.
Voor optellen van honderdtallen en duizendtallen kan je op soortgelijke wijze aan de slag.
Vier honderdtallen plus drie honderdtallen is samen zeven honderdtallen, oftewel \(400+300=700\). Je kunt honderdtallen dus optellen door gewoon zonder de laatste twee nullen op te tellen en er dan weer twee nullen achter te zetten. Immers, als je twee nullen achter een getal zet, dan maak je het honderdmaal zo groot.
Vier duizendtallen plus drie duizendtallen is samen zeven duizendtallen, oftewel \(4000+3000=7000\). Je kunt duizendtallen dus optellen door gewoon zonder de laatste drie nullen op te tellen en er dan weer drie nullen achter te zetten. Immers, als je twee nullen achter een getal zet, dan maak je het duizendmaal zo groot.
In onderstaande visualisatie van optellen hebben we de knikkers behouden, maar de bak waar ze in zitten weggelaten. Ook scheiden we de kolommen van tien knikkers van de kolom met minder dan tien knikkers door wat extra witruimte.
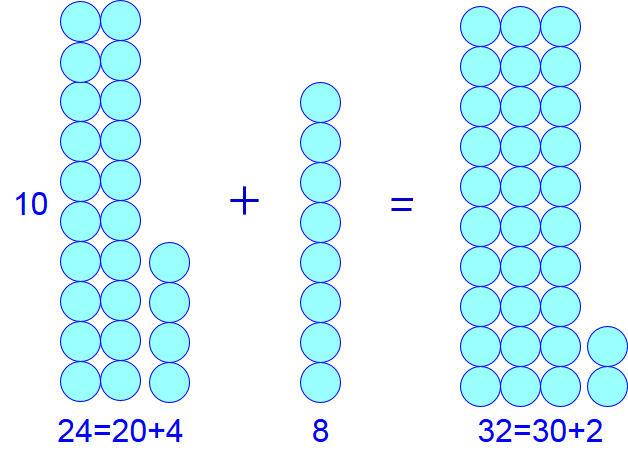
Als je \(24+8\) wilt uitrekenen, splits je \(24\) in \(20\) en \(4\). Omdat \(4+8=12\), geldt dan \(24+8=20+4+8=20+12=20+10+2=30+2\).
Onderstaande figuur hoort bij deze optelsom.
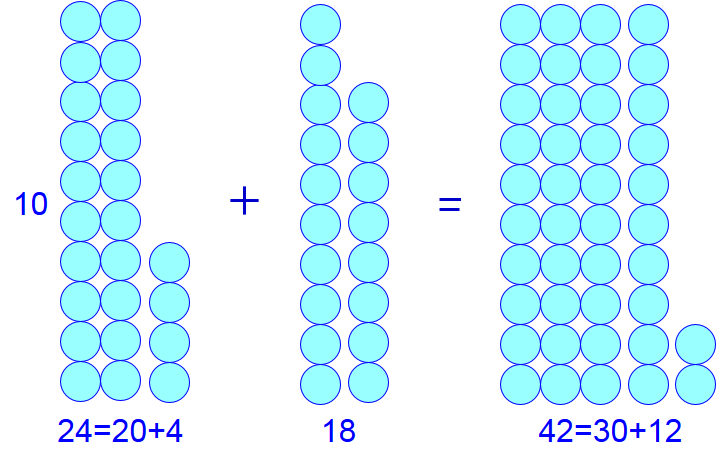
We bekijken nu hoe je twee getallen van twee cijfers bij elkaar op kunt tellen. Als voorbeeld nemen we \(24+18\). Het gaat in meerdere stappen:
- Reken eerst met de eenheden \(4+8=12\) en splits in dit geval \(12=10+2\).
- Reken nu met de tientallen \(20+10=30\)
- Tel nu de tussenresultaten bij elkaar op en vorm de uitkomst: \(30+12=30+10+2=42\)
Dit proces is hieronder gevisualiseerd
Optellen van natuurlijke getallen met pen en papier gaat het meest systematisch door de getallen rechts uitgelijnd onder elkaar te plaatsen en dan kolomsgewijs te rekenen. Bovenstaande optelling gaat dan volgens het volgende recept:
- Plaats de getallen rechts uitgelijnd onder elkaar: \[\begin{array}[t]{rl} 24 & \\ 18 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +}\end{array}\]
- Tel de eenheden (cijfer in de rechterkolom) op: \(4+8=12\) en van dit getal schrijf je alleen \(2\) op onder de streep en verhuis je de \(1\) naar de bovenkant van de volgende kolom (de tientallen).
- Tel de tientallen, dat wil zeggen de eerste cijfers van een 2-cijferig getal, met de extra \(1\) bij elkaar op: \(1+2+1=4\).
Het volgende schema illustreert de stappen in de berekening, waarbij we het extra toegevoegde cijfer bovenin op het laatst weer weghalen. \[\begin{aligned}
&\textit{Eenheden:}\qquad \\ \begin{array}[t]{rl} & \\ 2\blue{4} & \\ 1\blue{8} \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ \blue{1}\blue{2} & \end{array}
\quad &\longrightarrow\qquad \begin{array}[t]{rl} 1\phantom{2} & \\ 24 & \\ 18 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ 2 & \end{array} \\ \\
&\textit{Tientallen:}\qquad \\
\begin{array}[t]{rl} \blue{1}\phantom{2} & \\ \blue{2}4 & \\ \blue{1}8 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ \blue{4}2 & \end{array}
\quad &\longrightarrow\qquad \begin{array}[t]{rl} & \\ 24 & \\ 18 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ 42 & \end{array}
\end{aligned}\] Ervaren rekenaars schrijven de cijfers die we boven aan de kolommen geplaatst hebben niet meer op, maar onthouden ze en rekenen er direct mee door. Zij krijgen dan:
\[\begin{aligned} 4+8=12,\quad &\blue{2\text{ opschrijven, }1\text{ onthouden.}} \\ \blue{1}+2+1=4\phantom{2,} \quad &\blue{\text{Klaar. Uitkomst}=42.}\end{aligned}\] Opgeschreven in twee stappen, met hoofdrekenwerk en onthouden van het bijkomende tiental: \[\begin{array}[t]{r}\blue{\textit{stap 1:}} \\ \\ \\ \end{array}\quad \begin{array}[t]{rl} 24 & \\ 18 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ \phantom{4}2 & \end{array} \qquad \begin{array}[t]{r}\blue{\textit{stap 2:}} \\ \\ \\ \end{array}\quad \begin{array}[t]{rl} 24 & \\ 18 & \\ \overline{\phantom{xx}}& {}^{\displaystyle +} \\ 42 & \end{array}\]
Als je uit een bak met zeven knikkers driemaal één knikker weghaalt en deze in een tweede bak legt, dan heb je na afloop een tweede bak met drie knikkers en in de oorspronkelijke bak nog maar vier knikkers over. Onderstaand plaatje visualiseert het proces van het weghalen van drie knikkers uit een bak met zeven knikkers en het toevoegen van deze drie knikkers aan een tweede bak zonder knikkers aan het begin (de getekende ongekleurde ballen in de middelste bak geven slechts aan hoeveel knikkers er in terecht gaan komen).
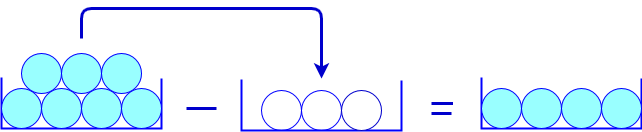
Je hebt in feite het getal \(3\) van \(7\) afgetrokken. Dit geef je aan met de gelijkheid \(7-3=4\) en spreek je uit als "zeven min drie is vier" of "zeven min drie is gelijk aan vier", al naar gelang of je de nadruk meer op de bewerking of op het getal vier wilt leggen.
De aftreksom \(3-7\) heeft binnen de natuurlijke getallen geen uitkomst omdat \(3\) kleiner is dan \(7\). Deze aftreksom heeft alleen betekenis binnen de gehele getallen en heeft dan als uitkomst het negatieve getal \(-4\). Wat je in feite doet is de twee getallen in de aftreksom te verwisselen: dan krijg je een aftreksom die wel binnen natuurlijke getallen op te lossen is. Vervolgens neem je het tegengestelde van het tussenresultaat.
Met knikkers in bakken kun je allerlei optellingen illustreren. Bijvoorbeeld \(4-0=4\), waarbij de middelste bak in het plaatje leeg blijft:

In het algemeen geldt dat een zeker getal min nul altijd gelijk is aan het getal waarmee je begon. In formuletaal: \[a-0=a\qquad\text{voor een willekeurig getal }a\text.\]
Als je weet dat \(7-3=4\) en hoe dit gevisualiseerd kan worden met knikkers in bakken, dan kan dat ook doen voor aftrekken van tientallen zoals bijvoorbeeld \(70-30\). Onderstaand plaatje visualiseert het proces van het weghalen van drie kolommen van tien knikkers uit een bak met zeven kolommen met tien knikkers en het toevoegen van deze drie kolommen van tien knikkers aan een tweede bak zonder knikkers aan het begin (de getekende ongekleurde ballen in de middelste bak geven slechts aan hoeveel knikkers er in terecht gaan komen). Je houdt dan in de oorspronkelijke bak vier kolommen met tien knikkers over.
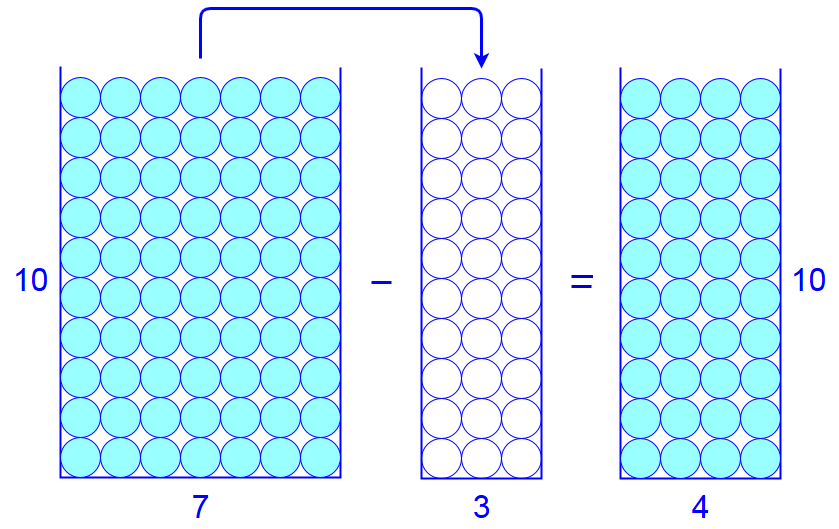
Zeven tientallen min drie tientallen is gelijk aan vier tientallen. Je kunt tientallen dus aftrekken door gewoon zonder nullen af te trekken en er dan weer een nul achter te zetten. Immers, als je een nul achter een getal zet, dan maak je het tienmaal zo groot.
Voor aftrekken van honderdtallen en duizendtallen kan je op soortgelijke wijze aan de slag.
Zeven honderdtallen min drie honderdtallen is gelijk aan vier honderdtallen, oftewel \(700-300=400\). Je kunt honderdtallen dus aftrekken door gewoon zonder de laatste twee nullen af te trekken en er dan weer twee nullen achter te zetten. Immers, als je twee nullen achter een getal zet, dan maak je het honderdmaal zo groot.
In onderstaande visualisatie van aftrekken hebben we de knikkers behouden, maar de bak waar ze in zitten weggelaten. Ook scheiden we de kolommen van tien knikkers van de kolom met minder dan tien knikkers door wat extra witruimte.
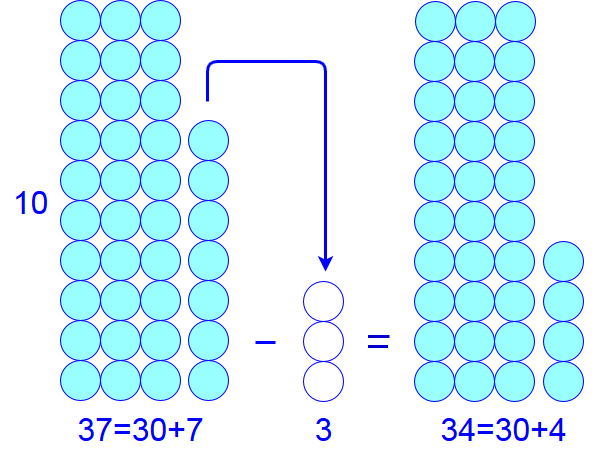
Als je \(37-3 \) wilt uitrekenen, splits je \(37\) in \(30\) en \(7\). Omdat \(7-3=4\), geldt dan \(37-3=30+7-3=30+4=34\). In feite trek je de eenheden van elkaar af.
Onderstaande figuur hoort bij deze aftreksom.
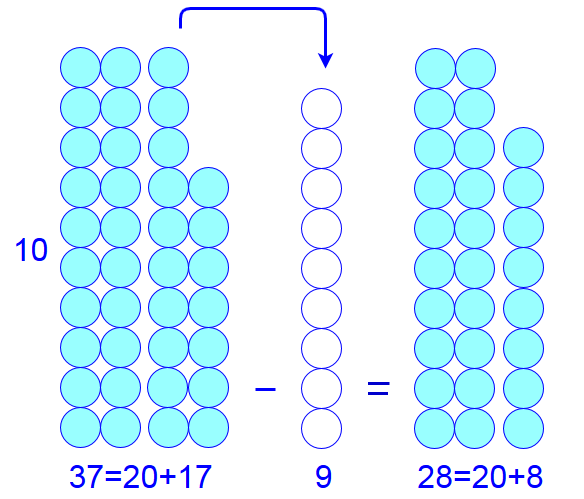
Maar wat kan je doen bij de aftreksom \(37-9\)? Nu kun je niet meer de eenheden van elkaar aftrekken, want \(7\) is kleiner dan \(9\). Opsplitsing van \(37\) in \(20+17\) biedt uitkomst. Omdat het tweede aantal knikkers klein is kun je \(17-9\) wel uitrekenen. Je neemt dan gewoon \(9\) knikkers van de stapel van \(17\) en houd er \(8\) over. Uiteraard hoor een dergelijke aftreksom uit het hoofd te kunnen. Deze aanpak er dus op neer dat je een tiental leent van de drie tientallen die je al hebt en twee tientallen ongemoeid laat. In onderstaande figuur is dit gevisualiseerd.
Aftrekken van twee natuurlijke getallen met pen en papier gaat het meest systematisch door de getallen rechts uitgelijnd onder elkaar te plaatsen en dan kolomsgewijs te rekenen. De aftreksom \(37-19\) gaat dan volgens het volgende recept:
- Plaats de getallen rechts uitgelijnd onder elkaar: \[\begin{array}[t]{rl} 37 & \\ 19 & \\ \overline{\phantom{xx}}& {}^{\displaystyle -}\end{array}\]
- Aftrekken van de eenheden (cijfer in de rechterkolom) gaat gelijk fout omdat \(7\) kleiner is dan \(9\). De oplossing is om een \(1\) te 'lenen' van het cijfer dat de tientallen aangeeft (en dat cijfer dus met \(1\) te verlagen). Je krijgt dan \(17-9=8\) als eenheid in het tussenresultaat.
- Trek de (aangepaste) tientallen van elkaar af: \(2-1=1\) wordt het tiental in het eindresultaat en samen met de eerder berekende eenheid heb je de uitkomst van de aftreksom systematisch bepaald.
Het volgende schema illustreert de stappen in de berekening, waarbij we het lenen van een 1 en het gevolg hiervan ook aangeven.
Eenheden: \[\begin{array}[t]{rl} \blue{2}\phantom{7}\\ \blue{3 {\kern -5pt /}}7 & \\ 19 & \\ \overline{\phantom{xxxxxx}}& {}^{\displaystyle -} \\ 8 & \end{array}\] Tientallen: \[\begin{array}[t]{rl} \blue{2}\phantom{7}\\ 3 {\kern -5pt /}7 & \\ \blue{1}9 & \\ \overline{\phantom{xxxxxx}}& {}^{\displaystyle -} \\ \blue{1}8 & \end{array}\] Dus: \(27-19=8\).
\(\phantom{x}\)
We geven een tweede voorbeeld, de aftreksom \(307-119\), waarin het cijfer waar je van moet lenen een \(0\) is. Je moet dan gewoon verderop aan de linkerkant een \(1\) lenen. In dit voorbeeld leen je dan van \(30\) en verander je \(30\) in \(29\). Onderstaand schema beschrijft de stappen in deze aftreksom.
Eenheden: \[\begin{array}[t]{rl} \blue{29}\phantom{7}\\\blue{3 {\kern -5pt /} 0 {\kern -5pt /}}7 & \\ 119 & \\ \overline{\phantom{xxxxxx}}& {}^{\displaystyle -} \\ 8 & \end{array}\] Tientallen: \[\begin{array}[t]{rl} \blue{29}\phantom{7}\\3 {\kern -5pt /} 0 {\kern -5pt /}7 & \\ 1\blue{1}9 & \\ \overline{\phantom{xxxxxx}}& {}^{\displaystyle -} \\ \blue{8}8 & \end{array}\] Honderdtallen: \[\begin{array}[t]{rl} \blue{29}\phantom{7}\\3 {\kern -5pt /} 0 {\kern -5pt /}7 & \\ \blue{1}19 & \\ \overline{\phantom{xxxxxx}}& {}^{\displaystyle -} \\ \blue{1}88 & \end{array}\] Dus: \(307-119=188\).
Als je drie kolommen van vier knikkers naast elkaar zet, heb je een structuur opgebouwd met in totaal \(3\times 4=12\) knikkers.
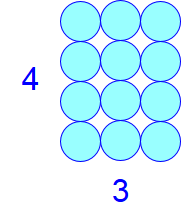
Dit illustreert dat vermenigvuldigen van natuurlijke getallen niet meer of minder is dan herhaald optellen: in ons voorbeeld geldt \(3\times 4=4+4+4=12\).
We spreken \(3\times 4=12\) uit als "drie keer vier is twaalf" of "drie maal vier is twaalf" wanneer we het accent willen leggen op het rekenwerk met het eindresultaat. Met de uitspraak "drie keer vier is gelijk aan twaalf" benadrukken we dat het gaat om equivalente voorstellingen van het getal twaalf: dit kan het cijfer \(12\) zijn en de uitkomst van de som \(3\times 4\), maar ook de uitkomst van bijvoorbeeld \(2\times 6\) of \(1\times 12\). De uitdrukkingen links en rechts zijn dan toegestane naamkaartjes voor hetzelfde wiskundige object.
Als je drie kolommen van vier knikkers naast elkaar zet, heb je een structuur opgebouwd met in totaal \(3\times 4=12\) knikkers. Andersom, als je vier kolommen van drie knikkers naast elkaar zet, dan heb je ook een structuur opgebouwd met in totaal \(4\times 3=12\) knikkers. Met andere woorden: \(4\times 3=3\times4\) en de uitkomst is ongeacht de volgorde van vermenigvuldigen gelijk aan \(12\).
In het algemeen geldt dat twee getallen in een product verwisseld mogen worden: dit heeft namelijk geen effect op de uitkomst van de bewerking. In formuletaal: \[a\times b=b\times a\qquad\text{voor willekeurige getallen }a\text{ en }b\tiny.\] Dit heet de commutatieve eigenschap van vermenigvuldigen van getallen, of wat minder deftig, de wisseleigenschap van vermenigvuldiging.
Als je bij berekeningen een precieze volgorde van bewerkingen wilt aangeven, dan moet je haakjes gebruiken. Bijvoorbeeld, \(4 \times (3\times 2)\) betekent eerst \(3\) en \(2\) vermenigvuldigen (tussenresultaat \(6\)), en vervolgens dit tussenresultaat met \(4\) vermenigvuldigen, hetgeen leidt tot de einduitkomst \(24\) als einduitkomst. Deze uitkomst is overigens ook gelijk aan die van de vermenigvuldiging in de gebruikelijk volgorde van links naar rechts [eerst \(4\) en \(3\) vermenigvuldigen (tussenresultaat \(12\)), en vervolgens vermenigvuldigen met \(2\)]. Met andere woorden: \((4\times 3)\times 2=4 \times (3\times 2)\).
In het algemeen geldt voor drie willekeurige getallen \(a\), \(b\) en \(c\): \[(a\times b)\times c=a\times (b\times c)\] Dit heet de associatieve eigenschap van vermenigvuldigen van getallen, of wat minder deftig, de schakeleigenschap van vermenigvuldiging van getallen.
De beide eigenschappen, namelijk de commutatieve en associatieve eigenschap, betekenen samen dat de volgorde waarin je natuurlijke getallen vermenigvuldigt niet uitmaakt voor de einduitkomst.
Omdat vermenigvuldigen van natuurlijke getallen eigenlijk herhaald optellen is, geldt bijvoorbeeld. Bijvoorbeeld \(4\times 0=0+0+0+0=0\).
In het algemeen geldt dat als je een zeker getal met nul vermenigvuldigt de uitkomst altijd gelijk is nul. In formuletaal: \[a\times 0=0\qquad\text{voor een willekeurig getal }a\tiny.\]
De distributieve eigenschap (minder deftig de verdeeleigenschap genoemd) is de eigenschap dat men de getallen in een bewerking als het ware ‘verdeelt’. Twee eenvoudige voorbeelden met een optelling resp. verschil en een vermenigvuldiging: \[3\times (10+4)=3\times 10+3\times 4\quad\text{en}\quad 3\times (10-4)=3\times 10-3\times 4\tiny.\] Met andere natuurlijke getallen gaat het net zo. Bijvoorbeeld, \((2+3)\times 4=2\times 4 + 3\times 4\). Het linkerlid kun je opvatten als de oppervlakte van een rechthoek met lengte \(2+3=5\) en breedte \(4\). De oppervlakte van deze rechthoek is gelijk aan de som van de oppervlakten van de twee kleinere rechthoeken in onderstaande figuur, met afmetingen van \(2\) bij \(4\) en \(3\) bij \(4\).
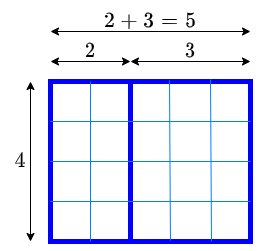
Dus geldt voor drie willekeurige natuurlijke getallen die we met de letter \(a\), \(b\) en \(c\) aanduiden in formuletaal: \[a\times (b+c)=a\times b + a\times c\quad\text{en}\quad a\times (b-c)=a\times b - a\times c\tiny.\] We zeggen ook wel dat de haakjes uitgewerkt zijn. Om dit gemakkelijker te onthouden kun je boogjes onder of boven plaatsen, bijvoorbeeld:
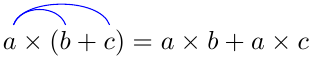
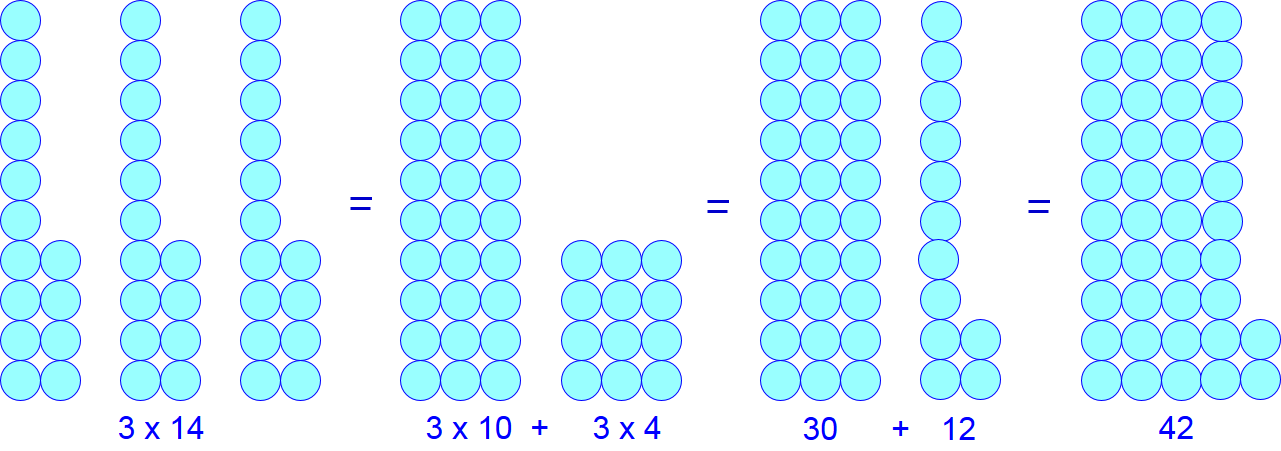
Met deze distributieve eigenschap kun je iets moeilijkere vermenigvuldigingsommen maken en visualiseren: \[\begin{aligned}3\times 14&=3\times(10+4)&\phantom{abcxyz} \blue{\text{splitsen van tientallen en eenheden}}\\ &=3\times 10+3\times 4&\phantom{abcxyz} \blue{\text{toepassen van de distributieve eigenschap}}\\ &=30+12&\phantom{abcxyz} \blue{\text{vermenigvuldigen van kleine getallen}}\\ &=42&\phantom{abcxyz} \blue{\text{optellen van natuurlijke getallen}}\end{aligned}\]
Omdat de letter \(x\) en het symbool \({}\times{}\) voor vermenigvuldigen erg op elkaar lijken, wordt vaak als alternatief een \({}\cdot{}\) gebruikt (in computeromgevingen of rekenmachines ook vaak een \({}*{}\)). Zelfs wordt, zolang er van geen verwarring kan ontstaan, het vermenigvuldigingsteken weggelaten bij formules met letters achteraan. Dus in plaats van \(2\times k\) of \(2\cdot k\) schrijft men kortweg \(2k\). Eigenschappen van vermenigvuldiging worden dan opgeschreven als \[ab=ba,\qquad (ab)c=a(bc), \qquad a(b+c)=ab+ac,\qquad\text{voor willekeurige getallen }a, b\text{ en }c\tiny.\]
Vermenigvuldigen van twee natuurlijke getallen met pen en papier gaat het meest systematisch door de getallen rechts uitgelijnd onder elkaar te plaatsen en dan kolomsgewijs te rekenen. De vermenigvuldigsom \(3\times 654\) gaat dan volgens het volgende recept:
- Plaats de getallen rechts uitgelijnd onder elkaar: \[\begin{array}[t]{rl} 654 & \\ 3 & \\ \overline{\phantom{xx}}& {}^{\displaystyle \times}\end{array}\]
- Vermenigvuldigen van de eenheden (cijfer in de rechterkolom) geeft \(3\times 4=12\).
- Vermenigvuldigen van de tientallen in het bovenste getal (cijfer in de middelste kolom) geeft \(3\times 50=150\).
- Vermenigvuldigen van het honderdtallen in het bovenste getal (cijfer in de linkerkolom) geeft \(3\times 600=1500\).
- Tel de tussenresultaten op en je hebt de uitkomst van de vermenigvuldigingssom systematisch bepaald: \(3\times 654=1500+150+12=1962\).
Je kunt de stappen ook in één keer kortsluiten: \[\begin{array}[t]{rl} 654 & \\ 3 & \\ \overline{\phantom{xxx}}& {}^{\displaystyle \times}\\ 2 & \end{array} \qquad \qquad\begin{array}[t]{rl} 654 & \\ 3 & \\ \overline{\phantom{xxx}}& {}^{\displaystyle \times}\\ 62 & \end{array} \qquad\qquad \begin{array}[t]{rl} 654 & \\ 3 & \\ \overline{\phantom{xxx}}& {}^{\displaystyle \times}\\ 1962 & \end{array} \] Toelichting: \[\begin{aligned} 3\times 4=12,\quad &\blue{2\text{ opschrijven, }1\text{ onthouden.}} \\ \blue{1}+3\times 5=16, \quad &\blue{6\text{ opschrijven, }1\text{ onthouden.}} \\ \blue{1}+3\times 6=19.\quad &\blue{\text{Klaar. Uitkomst}=1962.}\end{aligned}\]
Op deze manier lukt het altijd om een getal te vermenigvuldigen met een getal van één cijfer.
De vermenigvuldigingsom \(30\times 654\) kun je op een soortgelijke manier maken door in feite \(3\times 654=1962\) te bereken en aan dit tussenresultaat een slotnul toe te voegen.
De vermenigvuldigingsom \(23\times 654\) kun je in twee stappen uitvoeren: \(3\times 654=1962\) en \(20\times 654=13080\). Tel vervolgens de tussenresultaten op: \(1962+13080=15042\).
Samengevat: \[\begin{array}[t]{rlcr} 654 & & & \\ 23 & & & \\ \overline{\phantom{xxx}}& {}^{\displaystyle \times} & & \\ 1962 & & \blue{\leftarrow} & \blue{3\times 654}\\ 13080 & & \blue{\leftarrow} & \blue{20\times 654}\\ \overline{\phantom{xxx}}& {}^{\displaystyle +} & & \overline{\phantom{xxxxxxxx}} \\ 15042 & & \blue{\leftarrow} & \blue{23\times 654}\end{array}\]
Een laatste voorbeeld laat zien hoe het vermenigvuldigen met getallen van meer dan twee cijfers net zo georganiseerd kan worden. Bij alle tussenresultaten is rechts aangegeven hoe ze berekend zijn, maar in praktijk schrijf je dit niet uit. Dan werk je alleen met wat er links staat, maar let je wel op het plaatsen van de slotnullen die in blauw gemaakt zijn. \[\begin{array}[t]{rlcr} 654 & & & \\ 123 & & & \\ \overline{\phantom{xxx}}& {}^{\displaystyle \times} & & \\ 1962 & & \blue{\leftarrow} & \blue{3\times 654}\\ 1308\color{blue}{0} & & \blue{\leftarrow} & \blue{2\color{blue}{0}\times 654}\\ 654\color{blue}{00} & & \blue{\leftarrow} & \blue{1\color{blue}{00}\times 654}\\ \overline{\phantom{,xxxx}}& {}^{\displaystyle +} & & \overline{\phantom{xxxxxxx}} \\ 80442 & & \blue{\leftarrow} & \blue{123\times 654}\end{array}\]
\(\phantom{x}\)
Optellen, aftrekken en vermenigvuldigen van natuurlijke getallen gaat het meest systematisch door de getallen rechts uitgelijnd onder elkaar te plaatsen en dan kolomsgewijs te rekenen. Bekijk een paar voorbeelden en bestudeer zo nodig de extra uitleg onder de tabs in bovenstaande kaders.
Voer de volgende bewerking uit:
\[\begin{array}[t]{rl} 435 & \\ 69 & \\ 222 & \\ 95 & \\ 664 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +}\end{array}\]
Het correcte antwoord is \(1485\).
Optellen van dergelijke getallen leer je op de basisschool, maar misschien niet op de handigste en meest systematische manier. Het beste recept is als volgt:
- Plaats de getallen rechts uitgelijnd onder elkaar
- Tel de eenheden (cijfer in de rechterkolom) op: \(5+9+2+5+4=25\) en van dit getal schrijf je alleen \(5\) op onder de streep en verhuis je de \(2\) naar de bovenkant van de volgende kolom (de tientallen).
- Tel de tientallen, dat wil zeggen de middelste cijfers van een 3-cijferig getal, met de extra \(2\) bij elkaar op: \(2+3+6+2+9+6=28\). Ook nu schrijf je \(8\) onder de streep en verhuist \(2\) weer naar de bovenkant van de volgende kolom links.
- Tel de honderdtallen (met de extra \(2\) bij elkaar op: \(2+4+2+6=14\). Zet dat onder de streep en je bent klaar met de berekening met als uitkomst \(1485\).
Het volgende schema illustreert de stappen in de berekening, waarbij we de extra toegevoegde cijfers bovenin op het laatst weer weghalen
\[\begin{aligned}
&\textit{eenheden:}\qquad \\ \begin{array}[t]{rl} & \\ 43\blue{5} & \\ 6\blue{9} & \\ 22\blue{2} & \\ 9\blue{5} & \\ 66\blue{4} & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ \blue2\blue{5} & \end{array} \quad &\longrightarrow\qquad \begin{array}[t]{rl} \phantom{4}2\phantom{5} & \\ 435 & \\ 69 & \\ 222 & \\ 95 & \\ 664 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ 5 & \end{array}
\\ \\
&\textit{tientallen:}\qquad \\
\begin{array}[t]{rl} \phantom{4}\blue{2}\phantom{5} & \\ 4\blue{3}5 & \\ \blue{6}9 & \\ 2\blue{2}2 & \\ \blue{9}5 & \\ 6\blue{6}4 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ \blue2\blue{8}5 & \end{array} \quad &\longrightarrow\qquad \begin{array}[t]{rl} 22\phantom{5} & \\ 435 & \\ 69 & \\ 222 & \\ 95 & \\ 664 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ 85 & \end{array}
\\ \\
&\textit{honderdtallen:}\qquad \\
\begin{array}[t]{rl} \blue{2}2\phantom{5} & \\ \blue{4}35 & \\ 69 & \\ \blue{2}22 & \\ 95 & \\ \blue{6}64 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ \blue{14}85 & \end{array} \quad &\longrightarrow\qquad \begin{array}[t]{rl} \phantom{5} & \\ 435 & \\ 69 & \\ 222 & \\ 95 & \\ 664 & \\ \overline{\phantom{xxxx}}& {}^{\displaystyle +} \\ 1485 & \end{array}
\end{aligned}\]
Ervaren rekenaars schrijven de cijfers die we boven aan de kolommen geplaatst hebben niet meer op, maar onthouden ze en rekenen er direct mee door. Zij krijgen dan:
\[\begin{aligned} 5+9+2+5+4=25,\quad &\blue{5\text{ opschrijven, }2\text{ onthouden.}} \\ \blue{2}+3+6+2+9+6=28, \quad &\blue{8\text{ opschrijven, }2\text{ onthouden.}} \\ \blue{2}+4+2+6=14.\quad &\blue{\text{Klaar. Uitkomst}=1485.}\end{aligned}\]
\(\phantom{x}\)
Tot nu toe hebben we ons geconcentreerd op optellen, aftrekken en vermenigvuldiging van natuurlijke getallen. Dit vormt het fundament voor het rekenen met gehele getallen (die ook negatief kunnen zijn).
Aftreksommen binnen de gehele getallen zijn gemakkelijk te maken als je de volgende regel gebruikt:
Aftrekken van een getal is precies hetzelfde als optellen van het tegengestelde getal.
Bijvoorbeeld: \(1-3=1+(-3)=-2\).
De uitkomst is eenvoudig in te zien door de getallen voor te stellen als pijlen langs de getallenlijn en deze dan via de kop-staart methode aan elkaar te koppelen.

Productsommen binnen de gehele getallen zijn gemakkelijk te maken als je weet hoe je met \(-1\) moet vermenigvuldigen:
Vermenigvuldigen met \(-1\) is hetzelfde als het omklappen van het teken, van plus naar min of van min naar plus.
Bijvoorbeeld: \(3\times (-3)=3\times 3\times (-1)=9\times (-1)=-9\) en \((-3)\times (-4)=3\times (-1)\times 4\times (-1)=3\times 4\times (-1)\times (-1)=12\times (1)=12\).
In woorden samengevat en makkelijk te onthouden: \[\begin{array}{ll} \textit{plus keer plus is plus} & \textit{min keer plus is min} \\ \textit{plus keer min is min} & \textit{min keer min is plus}\end{array}\]
 Rekenkundige bewerkingen met gehele getallen
Rekenkundige bewerkingen met gehele getallen
![]()


![]()