Rekenen met getallen: Rekenen met gehele getallen
Deling met rest
Een deling die opgaat Als je \(24\) knikkers eerlijk wilt verdelen onder \(6\) kinderen, deel je \(4\) knikkers per kind uit en dan houd je niks over; immers, \(6\times 4=24\). Om uit te rekenen hoeveel knikkers je aan elk kind kunt geven kun je \(24\) delen door \(6\); in rekentaal schrijf je op \(24:6=4\) en spreek je dit uit als "vierentwintig gedeeld door zes is vier".
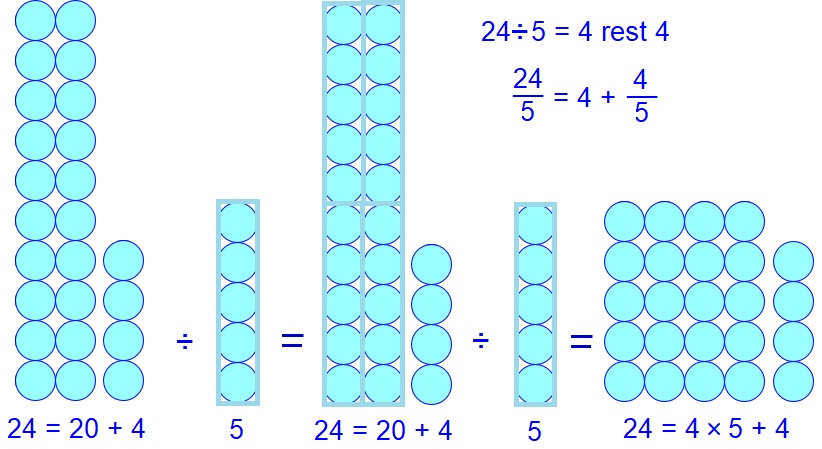
Deling met rest Maar wat te doen als je \(24\) knikkers eerlijk wilt verdelen onder \(5\) kinderen? Ook nu kun je beginnen met elk kind alvast \(4\) knikkers te geven. Dan heb je \(5\times 4=20\) knikkers uitgedeeld, maar zijn er nog \(4\) knikkers over. Als je deze overblijvende knikkers niet wilt verloten, dan blijf je met dit restant zitten. In rekentaal schrijf je op \(24:5=4\textit{ rest }4\) en spreek je dit uit als "vierentwintig gedeeld door vijf is vier rest vier".
Dit proces, waarbij een deling niet helemaal opgaat, heet delen met rest. In dit voorbeeld noemen we
- het aantal knikkers het deeltal;
- het aantal kinderen die knikkers krijgen de deler;
- het aantal knikkers dat elk kind krijgt het quotiënt;
- het aantal knikkers dat overblijft de rest.
Visualisatie We kunnen \(24\div 5=4\textit{ rest }4\) op onderstaande manier visualiseren, waarbij we nagaan hoe vaak het getal \(5\) past in \(24\). Dit kan namelijk viermaal en dan houd je nog 4 knikkers over. Dit betekent ook dat de breuk \(\frac{24}{5}\) te schrijven is als de som van \(4\) en \(\frac{4}{5}\). In gemengde breuknotatie is dit gelijk aan \(4\tfrac{4}{5}\).
De volgende stelling legt precies vast wat we bedoelen met deling met rest.
Deling met rest Als \(a\) en \(b\) natuurlijk getallen zijn en \(b>0\), dan zijn er unieke natuurlijke getallen \(q\) en \(r\) zodanig dat \[a=q \times b+r\qquad\text{en}\qquad 0\le r<b\text.\] Hierbij noemen we \(q\) het quotiënt en \(r\) de rest van de deling met rest van \(a\) door \(b\).
Het getal \(a\) heet deelbaar door \(b\) als de rest gelijk is aan nul. "De deling gaat op" en "\(b\) is een deler \(a\)", zeggen we in dit geval.
Staartdeling is de snelste en meest systematische aanpak voor het met pen en papier berekenen van de uitkomst van een deling of een deling met rest. Onderstaand groter voorbeeld illustreert dit.
Voorbeeld van staartdeling \[\begin{array}[t]{rrl}
36\; \Bigm/ \!\!\! & 81218 & \!\!\! \Bigm{\backslash} \; 2256 \\
& \underline{72}\phantom{000} & \qquad \blue{\uparrow}\\
& \phantom{0}92\phantom{00} & \blue{\text{quotiënt}}\\
& \phantom{0} \underline{72}\phantom{00} & \\
& \phantom{0}201\phantom{0} & \\
& \phantom{0}\underline{180}\phantom{0} & \\
& \phantom{00}218 & \\
& \phantom{00}\underline{216} & \\
& \phantom{0000}2 & \blue{ \leftarrow \text{rest}}
\end{array}\] Dus: \[81218= 2256\times 36 +2 \qquad\text{en}\qquad 81218:36 = 2256\textit{ rest }2\] Dit impliceert het volgende exacte resultaat van de deling: \[81218:36 =2256\tfrac{2}{36}=2256\tfrac{1}{18}\]
Instructievideo's Stichting Goed Rekenonderwijs
