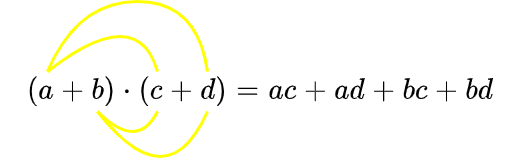De bananenformule om dubbele haakjes uit te werken

Rekenen met letters: Rekenen met letters

De bananenformule om dubbele haakjes uit te werken

De bananenformule

Voor het product van twee tweetermen, geldt de bananenformule:

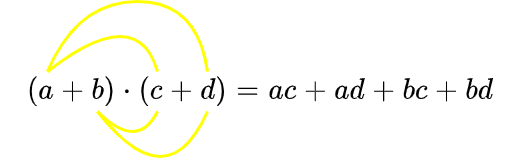
Voorbeelden

$\begin{aligned} (a+2)(b+3) &=a\cdot b+a\cdot 3+2\cdot b + 2\cdot 3\\ &= ab+3a+2b+6\\[0.3cm] (-4a+2)(2b-1) &= -4a\cdot 2b+-4a\cdot -1\\ &\phantom{=\,\,} +2\cdot 2b+2\cdot -1\\ &=-8ab+4a+4b-2\end{aligned}$

Zoals de banaanvormige boogjes al aangeven, ontstaat het rechterlid in de bananenformule door tweemaal een distributieve eigenschap te gebruiken: $\begin{aligned}(a+b)(c+d)&= a(c+d) + b(c+d)\\ &= ac +ad + bc + bd\end{aligned}$ Andere benamingen voor de eigenschap zijn de pagegaaienbekformule of krabbenschaarformule, vanwege de gelijkenis hiermee.

Soms kan het handig zijn een vermenigvuldigingstabel te gebruiken: $\begin{array}{c|c|c} \cdot & c & d\\ \hline a & ac & ad\\ \hline b & bc & bd \end{array}$ Na het invullen van het schema tel je de vier producten bij elkaar op.

De vermenigvuldigingstabel $\begin{array}{c|c|c|c} \cdot & d & e & f\\ \hline a & ad & ae & af\\ \hline b & bd & be & bf \\ \hline c & cd & ce & cf \end{array}$ laat zien dat het product van twee drietermen $(a+b+c)(d+e+f)$ uitgewerkt kan worden door elke term binnen het linkerpaar haakjes met elke term binnen het rechterpaar haakjes te vermenigvuldigen en vervolgens alle uitkomsten bij elkaar op te tellen: $\begin{aligned}(a+b+c)(d+e+f) \;=\; &\phantom{+}\; ad + ae + af \\ &+\; bd\, + be + bf \\ &+\; cd\, + ce + cf\end{aligned}$

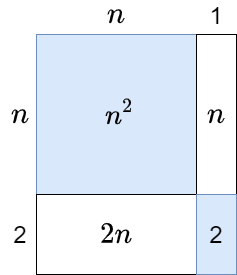
Een derde manier om de bananenformule voor te stellen is het oppervlaktemodel met rechthoeken. Bijvoorbeeld, de formule $(n+2)(n+1)=n^2+3n+1$ kan als volgt met rechthoeken gevisualiseerd worden:

Met de bananenformule kun je dubbele haakjes uitwerken. Een kwadraat van een tweeterm kun je hierbij zien als het product van twee identieke tweetermen. De formule kan ook in allerlei gecompliceerdere situaties gebruikt worden. Soms kun je na het uitwerken van haakjes m.b.v. de bananenformule nog termen samen nemen.

Werk in $(3c+6)(-3c-8)$ de haakjes uit.

$\begin{aligned}(3c+6)(-3c-8) &= (3c)\cdot (-3c)+(3c)\cdot (-8)+6\cdot (-3c)+6\cdot (-8)\\ &\phantom{abcdevwxyz}\blue{\text{de bananenformule}}\\ &= -9c^2-24c-18c-48\\ &\phantom{abcdevwxyz}\blue{\text{vereenvouding van termen}}\\ &=-9c^2-42c-48\\ &\phantom{abcdevwxyz}\blue{\text{gelijksoortige termen bij elkaar}}\end{aligned}$

Nieuw voorbeeld