The concept of quadratic function and parabola

Solving equations and inequalities: Quadratic equations

The concept of quadratic function and parabola

A basis form of a quadratic equation with unknown $x$ is

$ax^2+bx+c=0$ where $a$ , $b$ and $c$ are given numbers and $a\neq 0$ . The left-hand side of this equation can also by considered as a function definition of some function. This function is called a quadratic function. Solutions of a quadratic equation are therefore the zeros of the corresponding quadratic function. The graph of a quadratic function is called a parabola. A solutions of the quadratic equation is thus the $x$ coordinate of an intersection point of the corresponding parabola with the $x$ axis.

Definition and standard form of a quadratic function

A quadratic function or quadratic function with unknown $x$ has a function definition that can be reduced to the standard form

$f(x)=ax^2+bx+c$ where $a$ , $b$ and $c$ are given numbers and $a\neq 0$ .

In the examples on the right-hand side, the function definition of the same quadratic function $f(x)$ has been specified in different ways.

Examples

$\begin{aligned}f(x) &= x^2+3x+2\\[0.25cm] f(x)&=(x+\tfrac{3}{2})^2-\tfrac{1}{4}\\[0.25cm] f(x)&=(x+1)(x+2)\end{aligned}$

The graph of a quadratic function

The graph of a quadratic function is called a parabola. This consists of the points $(x,y)$ in the plane for which $y=ax^2+bx+c$ holds.

If $a>0$ , the graph is a valley parabola, i.e. a U-shaped graph that opens upward

If $a<0$ , the graph is a mountain parabola, i.e. an n-shaped graph that opens downward

The graphs below illustrate this naming.

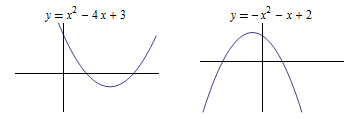
You can inspect other examples of parabolas by using the sliders in the figure on the right-hand side.

A valley parabola has a minimum and a mountain parabola has a maximum. In both cases, we call it the vertex of the parabola.
The $x$ -coordinate of the vertex is equal to $\displaystyle \frac{-b}{2a}$ .

Each parabola also has an axis of symmetry, namely, the vertical line through the vertex which separates the parabola in two halves that are each other's mirror image in a certain sense.

In the above two examples, the parabolas have two points in common with the horizontal axis. These are called the zeros or roots of the quadratic function.

A parabola has 0, 1 or 2 zeros.

GeoGebra

geometric definition

There is also a geometric definition of a parabola using a focous $F(p,q)$ and a directrix $y=r$ .

The parabola is the set of points in the plane having the same distance to the focus and to the directrix.

A point $(x,y)$ lies on the parabola when

$(x-p)^2+(y-q)^2=(y-r)^2$

In the parabola with basic form $y=ax^2+bx+c$ and discriminant $D=b^2-4ac$ , the coordinates of the focus and an equation of the directrix can be determined:

$\text{focus: }\left(-\frac{b}{2a}, \frac{-D+1}{4a}\right)\text{ and directrix: }y= \frac{-D-1}{4a}$

GeoGebra

$\phantom{x}$

Mathcentre video

Polynomial Functions (42:54)