Een tweedegraadsfunctie of kwadratische functie in de onbekende \(x\) heeft een functievoorschrift dat herleid kan worden tot de standaardvorm \[f(x)=ax^2+bx+c\] waarin \(a\), \(b\) en \(c\) gegeven getallen zijn en \(a\neq 0\).

In de voorbeelden aan de rechterkant is het functievoorschrift van een en dezelfde kwadratische functie \(f(x)\) op verschillende manieren opgeschreven.

Voorbeelden

\[\begin{aligned}f(x) &= x^2+3x+2\\[0.25cm] f(x)&=(x+\tfrac{3}{2})^2-\tfrac{1}{4}\\[0.25cm]
f(x)&=(x+1)(x+2)\end{aligned}\]

De grafiek van een kwadratische functie heet een parabool. Deze bestaat uit de punten \((x,y)\) in het vlak waarvoor \(y=ax^2+bx+c\).

Als \(a>0\), dan is de grafiek een dalpa‍rabool.

Als \(a<0\), dan is de grafiek een bergpa‍rabool.

Onderstaande grafieken illustreren deze benaming.

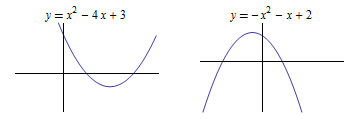
In de figuur rechts kunnen andere voorbeelden bekeken worden door de schuifbalken naar wens in te stellen

Een dalparabool heeft een minimum en een bergparabool heeft een maximum. In beide gevallen noemen we dit de top van de parabool.
De \(x\)-coördinaat van de top is gelijk aan \(\displaystyle \frac{-b}{2a}\).

Elke parabool heeft ook een symmetrieas, namelijk de verticale lijn door de top die de parabool scheidt in twee helften die in een bepaalde zin elkaars spiegelbeeld zijn.

In bovenstaande twee voorbeelden hebben de parabolen twee punten gemeen met de horizontale as. Dit heten de nulpunten of wortels van de kwadratische functie.

Een parabool heeft 0, 1 of 2 nulpunten.