Solving quadratic inequalities via reduction and/or factorization

Solving equations and inequalities: Quadratic inequalities

Solving quadratic inequalities via reduction and/or factorization

The steps in solving a quadratic inequality with one unknown via reduction are the same as in solving a quadratic equation by reduction:

addition or subtraction of the same term on both sides;
multiplication or division by the same nonzero number on both sides;
Combination of similar terms.

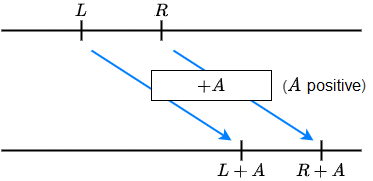
$L<R$ is equivalent to
$L+A<R+A$ and $L-A<R-A$

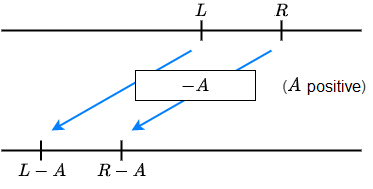
$L>R$ is equivalent to
$L+A>R+A$ and $L-A>R-A$

Here, $A$ is an arbitrary expression.

Example
$\begin{aligned} 4x^2+1&>5\\[0.25cm] 4x^2+1-1&>5-1\\[0.25cm] 4x^2&>4\end{aligned}$

Inequalities ≤ or ≥ The rule also applies to inequalities $\le$ or $\ge$ ; In fact, this involves a combination of an inequality $\lt$ or $\gt$ and a quadratic equation, for which the rule also holds. For example: $\begin{aligned} 4x^2+1&\ge 5\\[0.25cm] 4x^2+1-1&\ge 5-1\\[0.25cm] 4x^2&\ge 4\end{aligned}$

Whether or not an equivalence symbool The reduction is based on equivalence of inequalities and you can use the double implicaton arrows $\Leftrightarrow$ . You write for example $\begin{aligned} 4x^2+1 \ge 5 &\Leftrightarrow 4x^2+1-1 \ge 5-1\\[0.25cm] &\Leftrightarrow 4x^2\ge 4\\[0.25cm]&\Leftrightarrow x^2\ge 1\end{aligned}$ But because of the stepwise structured reduction it is often enough to place consecutive equivalent expressions on separate lines, omitting the equivalence symbol. Then you get $\begin{aligned} 4x ^ 2 + 1 &\ge 5 \\[0.25cm] 4x^2+1-1&\ge 5-1\\[0.25cm] 4x^2&>4\\[0.25cm] x^2&>1\end{aligned}$

Visualisation If you substitute a solution for $x$ in the inequality $L<R$ , then $L$ and $R$ become numbers, of which $L$ is to the left of $R$ on the number line. When you add or subtract on both sides of the inequality a number $A$ nothing changes in the relative position of the numbers.

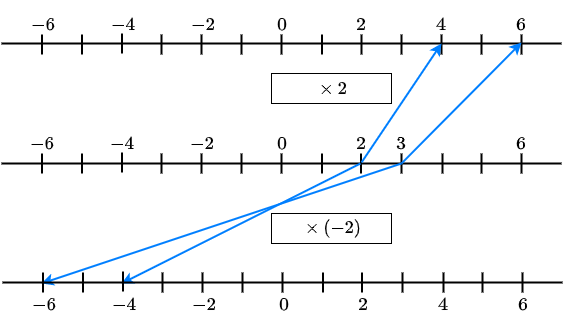
If $A>0$ , then $L<R$ is equivalent to
$A\cdot L<A\cdot R$ and $\dfrac{L}{A}<\dfrac{R}{A}$

If $A>0$ , then $L>R$ is equivalent to
$A\cdot L>A\cdot R$ and $\dfrac{L}{A}>\dfrac{R}{A}$

If $A<0$ , then $L<R$ is equivalent to
$A\cdot L>A\cdot R$ and $\dfrac{L}{A}>\dfrac{R}{A}$

If $A<0$ , then $L>R$ equivalent is to
$A\cdot L<A\cdot R$ and $\dfrac{L}{A}<\dfrac{R}{A}$

Here, $A$ is an arbitrary nonzero number.

Examples
$\begin{aligned} -x^2&< 1\\[0.25cm] (-1)\cdot (-x^2)&\gt(-1)\cdot 1\\[0.25cm] x^2&\gt -1\\[0.75cm]-2x^2&>8\\[0.25cm]\dfrac{-2x^2}{-2}&<\dfrac{8}{-2}\\[0.25cm] x^2&<4\end{aligned}$

Inequalities ≤ or ≥ The rule also applies to inequalities $\le$ or $\ge$ ; In fact, this involves a combination of an inequality $\lt$ or $\gt$ , and a linear equation, for which the rule applies too.
Thus, when multiplying or dividing by a negative number, the inequality sign $\le$ is replaced by $\ge$ , and $\ge$ is replaced by $\le$ ; The inequality sign 'flips'. For example: $\begin{aligned} -x^2&\le 1\\[0.25cm] (-1)\cdot (-x^2)&\ge(-1)\cdot 1\\[0.25cm] x^2&\ge -1\\[0.75cm]-2x^2&\ge -8\\[0.25cm]\dfrac{-2x^2}{-2}&\le\dfrac{-8}{-2}\\[0.25cm] x^2&\le 4\end{aligned}$

visualization

If you substitute a solution for $x$ in the inequality $L<R$ , then $L$ and $R$ become numbers, of which $L$ is to the left of $R$ on the number line. When you multiply the two numbers by a number $A$ or divide by $A$ , it depends on the sign of $A$ whether or not the relative position of the numbers on the number line changes.

For example, suppose that you get after substitution of $x$ the numbers $L=2$ and $R=3$ . Then you have $L<R$ and $L$ is located on the number line to the left of $R$ . If you multiply the left and right in the inequality by $2$ , you get $4<6$ and that is true. But if you had instead multiplied the left-hand and right-hand side in the inequality by $-2$ you would have gotten $-4<-6$ and that is incorrect; The true statement is $-4>-6$ and the inequality sign 'flips' because the number that was first to the left on the number line has now become a number to the right.

With the above rules, you can solve quadratic inequalities, i.e., reduce to an inequality in which the unknown is isolated and on the left-hand side of a inequality. Completing the square and factorisation by inspection are often productive strategies.

Suppose that reduction and completing the square has led to the inequality $a(x+p)^2+q<0$ for certain real numbers $a$ , $p$ , $q$ with $a\neq 0$ .

If $a>0$ , then this is equivalent to the inequality $(x+p)^2<\dfrac{q}{a}$ . We distinguish three cases:

if $q<0$ , then there are no solutions.
as $q=0$ , then $x=-p$ is the only solution.
as $q>0$ , then $-\sqrt{\dfrac{q}{a}}<x+p<\sqrt{\dfrac{q}{a}}$ , that is $-p-\sqrt{\dfrac{q}{a}}<x<-p+\sqrt{\dfrac{q}{a}}$

If $a<0$ then this is equivalent to the inequality $(x+p)^2>\dfrac{q}{a}$ . We distinguish three cases:

if $q<0$ then all real numbers satisfy the inequalite because a square of a real number is always greater than or equal to $0$ .
as $q=0$ , then $x=-p$ the only solution.
as $q>0$ , then $x+p<-\sqrt{\dfrac{q}{a}}\;\vee x+p>\sqrt{\dfrac{q}{a}}$ , that is $x<-p-\sqrt{\dfrac{q}{a}}\;\vee\;x<-p+\sqrt{\dfrac{q}{a}}$

Suppose that you can write the inequality as $a(x+p)(x+q)>0$ for certain real numbers $a$ , $p$ , $q$ with $a\neq 0$ .

If $a>0$ , then this is equivalent to the inequality $(x+p)(x+q)>0$ . We distinguish two cases:

if $x+p>0$ and $x+q>0$ , then $x>-p$ and $x>-q$ , that is $x>\max(-p,-q)$ .
if $x+p<0$ and $x+q<0$ , then $x<-p$ and $x<-q$ , that is $x<\min(-p,-q)$ .

If $a<0$ , then the inequality is equivalent to $(x+p)(x+q)<0$ with solution $\min(-p,-q)<x<\max(-p,-q)$ .

Illustrative examples:

Determine the exact real solution of the following quadratic inequality by completing the square. $2x^2-6x+10<0$

We work out the method of completing the square: $\begin{aligned} 2x^2-6x+10<0 & \phantom{abcxyz} \blue{\text{the given quadratic inequality}} \\ \\ x^2-3x+5<0 & \phantom{abcxyz} \blue{\text{division by }2\text{ on both sides}} \\ \\ \left(x-{{3}\over{2}}\right)^2-\left(-{{3}\over{2}}\right)^2+5<0 &\phantom{abcxyz} \blue{\text{completing the square}}\\ \\ \left(x-{{3}\over{2}}\right)^2+{{11}\over{4}}<0& \phantom{abcxyz} \blue{\text{simplification}}\\ \\ \left(x-{{3}\over{2}}\right)^2<-{{11}\over{4}}& \phantom{abcxyz} \blue{\text{isolation of the square term}}\\ \\ \text{no solution} & \blue{\phantom{abcxyz}\text{the square of a real number cannot be negative}} \end{aligned}$

New example