Oplossen van tweedegraadsongelijkheden via herleiding en/of ontbinding in factoren

Vergelijkingen en ongelijkheden oplossen: Tweedegraadsongelijkheden met één onbekende

Oplossen van tweedegraadsongelijkheden via herleiding en/of ontbinding in factoren

De stappen in het oplossen van een tweedegraadsongelijkheid met één onbekende door herleiding zijn dezelfde als bij het oplossen van een tweedegraadsvergelijking via herleiding:

aan beide zijden dezelfde term optellen of aftrekken;
beide zijden met hetzelfde getal ongelijk aan nul vermenigvuldigen of delen;
gelijksoortige termen samenvoegen.

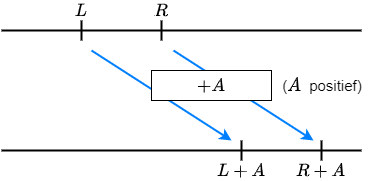
$L<R$ is gelijkwaardig met
$L+A<R+A$ en met $L-A<R-A$

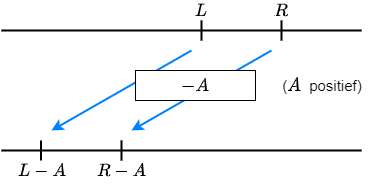
$L>R$ is gelijkwaardig met
$L+A>R+A$ en met $L-A>R-A$

Hierbij is $A$ een willekeurige uitdrukking.

Voorbeeld
$\begin{aligned} 4x^2+1&>5\\[0.25cm] 4x^2+1-1&>5-1\\[0.25cm] 4x^2&>4\end{aligned}$

Ongelijkheden met kleiner (groter) dan of gelijk aan De regel geldt ook voor ongelijkheden met $\le$ of $\ge$ ; in feite gaat het hierbij om een samenstelling van een ongelijkheid met $\lt$ of $\gt$ en een tweedegraadsvergelijking, waarvoor de regel ook geldt. Bijvoorbeeld: $\begin{aligned} 4x^2+1&\ge 5\\[0.25cm] 4x^2+1-1&\ge 5-1\\[0.25cm] 4x^2&\ge 4\end{aligned}$

Wel of geen equivalentiesymbool De herleiding is gebaseerd op equivalentie van ongelijkheden en het gebruik van dubbele implicatiepijlen $\Leftrightarrow$ is dus toepasselijk. Je schrijft dan in het voorbeeld $\begin{aligned} 4x^2+1 \ge 5 &\Leftrightarrow 4x^2+1-1 \ge 5-1\\[0.25cm] &\Leftrightarrow 4x^2\ge 4\\[0.25cm]&\Leftrightarrow x^2\ge 1\end{aligned}$ Maar door de stapsgewijze, gestructureerde herleiding wordt vaak volstaan met het plaatsen van opeenvolgende equivalente uitdrukkingen op aparte regels, met weglating van het equivalentiesymbool. Je krijgt dan dus $\begin{aligned} 4x^2+1&\ge 5 \\[0.25cm] 4x^2+1-1&\ge 5-1\\[0.25cm] 4x^2&>4\\[0.25cm] x^2&>1\end{aligned}$

Visualisatie Als je voor $x$ in de ongelijkheid $L<R$ een oplossing invult, dan worden $L$ en $R$ getallen waarbij $L$ links van $R$ ligt op de getallenlijn. Als je bij beide getallen $A$ optelt of aftrekt verandert er niets aan de onderlinge positie.

Als $A>0$ , dan is $L<R$ is gelijkwaardig met
$A\cdot L<A\cdot R$ en met $\dfrac{L}{A}<\dfrac{R}{A}$

Als $A>0$ , dan is $L>R$ is gelijkwaardig met
$A\cdot L>A\cdot R$ en met $\dfrac{L}{A}>\dfrac{R}{A}$

Als $A<0$ , dan is $L<R$ is gelijkwaardig met
$A\cdot L>A\cdot R$ en met $\dfrac{L}{A}>\dfrac{R}{A}$

Als $A<0$ , dan is $L>R$ is gelijkwaardig met
$A\cdot L<A\cdot R$ en met $\dfrac{L}{A}<\dfrac{R}{A}$

Hierbij is $A$ een willekeurig getal ongelijk aan nul.

Voorbeelden
$\begin{aligned} -x^2&< 1\\[0.25cm] (-1)\cdot (-x^2)&\gt(-1)\cdot 1\\[0.25cm] x^2&\gt -1\\[0.75cm]-2x^2&>8\\[0.25cm]\dfrac{-2x^2}{-2}&<\dfrac{8}{-2}\\[0.25cm] x^2&<4\end{aligned}$

Ongelijkheden met kleiner (groter) dan of gelijk aan De regel geldt ook voor ongelijkheden met $\le$ of $\ge$ ; in feite gaat het hierbij om een samenstelling van een ongelijkheid met $\lt$ of $\gt$ en een eerstegraadsvergelijking, waarvoor de regel ook geldt.
Dus bij vermenigvuldigen met of delen door een negatief getal wordt het vergelijkingsteken $\le$ vervangen door $\ge$ en wordt $\ge$ vervangen door $\le$ ; het vergelijkingsteken klapt als het ware om. Bijvoorbeeld: $\begin{aligned} -x^2&\le 1\\[0.25cm] (-1)\cdot (-x^2)&\ge(-1)\cdot 1\\[0.25cm] x^2&\ge -1\\[0.75cm]-2x^2&\ge -8\\[0.25cm]\dfrac{-2x^2}{-2}&\le\dfrac{-8}{-2}\\[0.25cm] x^2&\le 4\end{aligned}$

Visualisatie

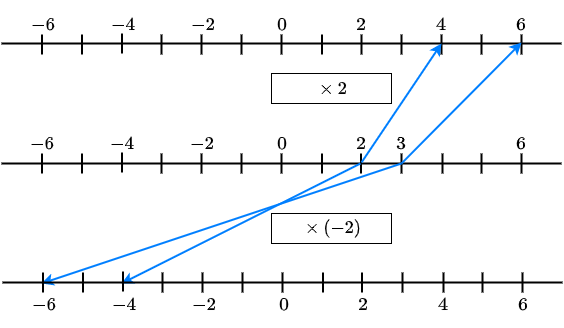
Als je voor $x$ in de ongelijkheid $L<R$ een oplossing invult, dan worden $L$ en $R$ getallen waarbij $L$ links van $R$ ligt op de getallenlijn. Als je beide getallen vermenigvuldigt met een getal $A$ of deelt door $A$ , hangt het van het teken van $A$ af of de onderlinge positie op de getallenlijn wel of niet verandert.

Stel bijvoorbeeld dat je na substitutie van $x$ uitkomt op $L=2$ en $R=3$ . Dan geldt dus $L<R$ en ligt $L$ links van $R$ ligt op de getallenlijn. Als je in de ongelijkheid links en recht vermenigvuldigt met $2$ , krijg je $4<6$ en dat is waar. Maar had je in plaats daarvan links en rechts in de ongelijkheid met $-2$ vermenigvuldigt, dan krijg je $-4<-6$ en dat is onjuist; de ware bewering is $-4>-6$ en het vergelijkingsteken 'klapt om' omdat het getal dat eerst het meest links op de getallenlijn lag nu juist het meest rechts komt te liggen.

Met bovenstaande regels kun je kwadratische ongelijkheden oplossen, dat wil zeggen herleiden tot een ongelijkheid waarin de onbekende geïsoleerd is en links in een ongelijkheid staat. Kwadraatsafsplitsing en ontbinding in factoren is hierbij handig.

Stel dat je door herleiding uitgekomen bent op de ongelijkheid $a(x+p)^2+q<0$ voor zekere reële getallen $a$ , $p$ , $q$ en $a\neq 0$ .

Als $a>0$ dan is dit equivalent met de ongelijkheid $(x+p)^2<\dfrac{q}{a}$ . We onderscheiden drie gevallen:

als $q<0$ , dan zijn er geen oplossingen.
als $q=0$ , dan is $x=-p$ de enige oplossing.
als $q>0$ , dan $-\sqrt{\dfrac{q}{a}}<x+p<\sqrt{\dfrac{q}{a}}$ , oftewel $-p-\sqrt{\dfrac{q}{a}}<x<-p+\sqrt{\dfrac{q}{a}}$

Als $a<0$ dan is dit equivalent met de ongelijkheid $(x+p)^2>\dfrac{q}{a}$ . We onderscheiden drie gevallen:

als $q<0$ voldoen alle reële getallen omdat een kwadraat van een reëel getal altijd groter dan of gelijk aan $0$ is.
als $q=0$ , dan is $x=-p$ de enige oplossing.
als $q>0$ , dan $x+p<-\sqrt{\dfrac{q}{a}}\;\vee x+p>\sqrt{\dfrac{q}{a}}$ , oftewel $x<-p-\sqrt{\dfrac{q}{a}}\;\vee\;x<-p+\sqrt{\dfrac{q}{a}}$

Stel dat je de ongelijkheid kunt schrijven als $a(x+p)(x+q)>0$ voor zekere reële getallen $a$ , $p$ , $q$ en $a\neq 0$ .

Als $a>0$ , dan is dit equivalent met de ongelijkheid $(x+p)(x+q)>0$ . We onderscheiden twee gevallen:

als $x+p>0$ en $x+q>0$ , dan moet $x>-p$ en $x>-q$ , oftewel $x>\max(-p,-q)$ .
als $x+p<0$ en $x+q<0$ , dan moet $x<-p$ en $x<-q$ , oftewel $x<\min(-p,-q)$ .

Als $a<0$ , dan is de ongelijkheid equivalent met $(x+p)(x+q)<0$ met als oplossing $\min(-p,-q)<x<\max(-p,-q)$ .

Enkele voorbeelden ter illustratie:

Bereken exact de reële oplossing van onderstaande kwadratische ongelijkheid via kwadraatsafsplitsing. $3x^2+24x-3<0$

We schrijven de methode van kwadraatafsplitsen uit: $\begin{aligned} 3x^2+24x-3<0 & \phantom{abcxyz} \blue{\text{de gegeven kwadratische ongelijkheid}} \\ \\ x^2+8x-1<0 & \phantom{abcxyz} \blue{\text{deling door }3\text{ aan weerszijden}} \\ \\ \left(x+4\right)^2-4^2-1<0 &\phantom{abcxyz} \blue{\text{afsplitsing van een kwadraat}}\\ \\ \left(x+4\right)^2-17<0& \phantom{abcxyz} \blue{\text{vereenvoudiging}}\\ \\ \left(x+4\right)^2<17& \phantom{abcxyz} \blue{\text{isolatie van het kwadraat}}\\ \\ x+4<\sqrt{17}\quad \land \quad x+4>-\sqrt{17} & \blue{\phantom{abcxyz}\text{twee oplossingen met worteltrekken}} \\ \\ -4-\sqrt{17}\lt x \lt -4+\sqrt{17} & \blue{\phantom{abcxyz}\text{eindantwoord}} \end{aligned}$

Nieuw voorbeeld