Gewone differentiaalvergelijkingen: Bifurcaties
Bifurcaties en bifurcatiediagrammen
We bekijken de differentiaalvergelijking \[\frac{\dd y}{\dd t}=f(y,b)\] waarbij \(f\) een zekere functie is en \(b\) een parameter. In onderstaande figuur is de grafiek van het rechterlid van de differentiaalvergelijking als functie van \(y\) getekend zijn voor 4 verschillende parameterwaarden, namelijk voor \(b=-10\), \(b=-4\), \(b=2\) en \(b=10\). Voor \(b\)-waarden tussen \(-10\) en \(10\) verandert de functie netjes zodat de grafiek steeds netjes tussen de getoonde grafieken zal liggen.
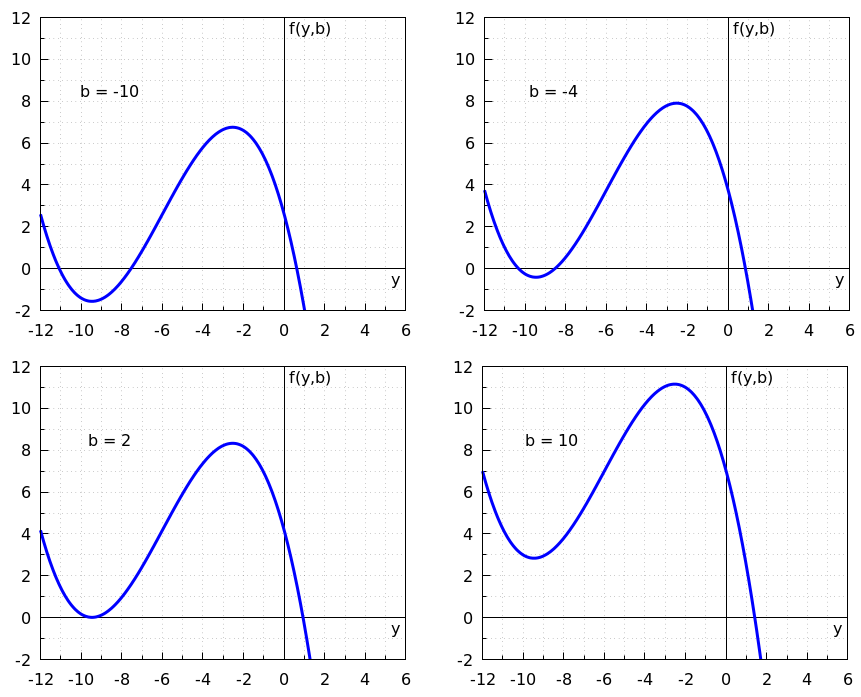
Welke bifurcatiewaarde, te noemen \(b^{\ast}\!\), is uit de getoonde grafieken af te leiden?
\(b^{\ast}={}\)
Bij de bifurcatie verandert het aantal evenwichten:
Voor \(-10\le b< b^{\ast}\) is het aantal evenwichten gelijk aan
Voor \(\phantom{-}b^{\ast}\lt b \lt 10 \) is het aantal evenwichten gelijk aan
Selecteer de juiste elementen uit onderstaande rolmenu's zodat je de toestandslijn van deze differentiaalvergelijking krijgt bij de bifurcatiewaarde \(b^{\ast}\!\).
\(b^{\ast}={}\)
Bij de bifurcatie verandert het aantal evenwichten:
Voor \(-10\le b< b^{\ast}\) is het aantal evenwichten gelijk aan
Voor \(\phantom{-}b^{\ast}\lt b \lt 10 \) is het aantal evenwichten gelijk aan
Selecteer de juiste elementen uit onderstaande rolmenu's zodat je de toestandslijn van deze differentiaalvergelijking krijgt bij de bifurcatiewaarde \(b^{\ast}\!\).
Ontgrendel volledige toegang
