Complexe getallen: Het complexe vlak
 Complexe getallen als vectoren
Complexe getallen als vectoren
Meetkundig rekenen met complexe getallen gaat gemakkelijker als je complexe getallen niet ziet als punten in het complexe vlak maar als vectoren.
Een vector in een coördinatenvlak kun je je voorstellen als een pijl die van een beginpunt naar een eindpunt loopt. Evenwijdige pijlen met dezelfde richting en dezelfde grootte stellen dezelfde vector voor. We spreken van een positievector als het beginpunt gelijk is aan de oorsprong van het coördinatenstelsel. Voor vectoren kun je een som en verschil definiëren; onderstaande dynamische figuren illustreren dit.
Optellen en aftrekken van vectoren Twee positievectoren kun je bij elkaar optellen en het resultaat is weer een positievector, die verkregen wordt via de constructie van een paralellogram:
Verplaats \(\vec{v}\) en/of \(\vec{w}\) om te zien hoe optellen van positievectoren gaat.
Twee positievectoren kun je van elkaar aftrekken en het resultaat is weer een positievector, die verkregen wordt via de constructie van een paralellogram:
Verplaats \(\vec{v}\) en/of \(\vec{w}\) om te zien hoe aftrekken van positievectoren gaat.
Een positievector \(\vec{v}\) met eindpunt \((v_1,v_2)\) noteren we vaak als \(\begin{pmatrix} v_1 \\ v_2\end{pmatrix}\).
De volgende regel laat in deze notatie zien dat optelling van vectoren componentsgewijs verloopt.
Als \(\vec{v}=\!\!\begin{pmatrix} v_1 \\ v_2\end{pmatrix}\) en \(\vec{w}=\!\!\begin{pmatrix} w_1 \\ w_2\end{pmatrix}\), dan \(\vec{v}+\vec{w} = \!\!\begin{pmatrix} v_1+w_1 \\ v_2+w_2\end{pmatrix}\).
Laten we nu eens kijken wat vectoren en complexe getallen met elkaar te maken hebben.
Optellen en aftrekken van complexe getal in meetkundig perspectief In het complexe vlak kun je bij elk complex getal \(\alpha\) een positievector maken door een pijl te tekenen die van de oorsprong naar het punt \(\alpha\) in het complexe vlak loopt. Deze positievector kan ook worden voorgesteld door een vector die in een willekeurig punt \(\beta\) start en naar het punt \(\alpha+\beta\) loopt; de punten \(0,\) \(\alpha,\) \(\beta\) en \(\alpha+\beta\) vormen samen een parallellogram. Zie onderstaande figuur.
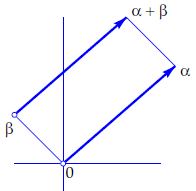
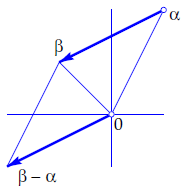
De vectorvoorstelling van complexe getallen is dus zo handig omdat optelling van complexe getallen correspondeert met optelling van vectoren. De vectorvoorstelling is ook handig als je het verschil \(\beta-\alpha\) van twee complexe getallen \(\alpha\) en \(\beta\) in beeld wilt brengen: \(\beta-\alpha\) is de positievector die past bij de pijl die van \(\alpha\) naar \(\beta\) loopt. Ook nu kan weer een parallellogram gebruikt worden:
Bewerkingen met complexe getallen hebben regelmatig een meetkundige betekenis. Hieronder zie je wat er gebeurt als je een complex getal, passend bij vector \(\vec{v}\), met \(\mathrm{i}\) vermenigvuldigd. Verplaats \(\vec{v}\) en zoek zo uit wat de meetkundige interpretatie van complexe vermenigvuldiging met \(\mathrm{i}\) in het complexe vlak is.
Inderdaad: vermenigvuldiging met de imaginaire eenheid \(\mathrm{i}\) in het complexe vlak heeft de meetkundige betekenis van rotatie tegen de wijzers van de klok in over 90 graden.


