Complexe getallen op de eenheidscirkel

Complexe getallen: Het complexe vlak

Complexe getallen op de eenheidscirkel

We brengen in herinnering dat de eenheidscirkel gedefinieerd is als de cirkel met straal \(1\) en de oorsprong als middelpunt. We gaan nu complexe getallen bekijken die op de eenheidscirkel in het complexe vlak liggen.

Elk punt op de eenheidscirkel heeft coördinaten die geschreven kunnen worden als \((\cos\varphi,\sin\varphi)\), waarbij \(\varphi\) de georiënteerde hoek is die de voerstraal (de verbindingslijn van het punt met de oorsprong) maakt met de positieve \(x\)-as. Hierbij gebruiken we radialen en de hoek is dan op gehele veelvouden van \(2\pi\) na bepaald.

Als complex getal geschreven, is een punt op de eenheidscirkel dus altijd te schrijven in de vorm \[z=\cos\varphi + \mathrm{i} \sin\varphi\]

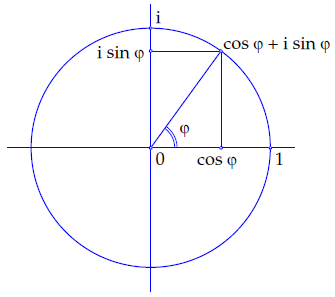
eenheidscirkel in het complexe vlak

Merk op dat inderdaad voor zo'n getal geldt dat \[|\cos\varphi + \mathrm{i} \sin\varphi|=\sqrt{\cos^2\varphi +\sin^2\varphi}=\sqrt{1}=1\]

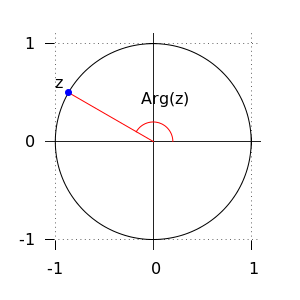
Argument De hoek \(\varphi\) van het complexe getal \(z=\cos\varphi + \mathrm{i} \sin\varphi\) heet het argument van \(z\) en wordt genoteerd als \(\mathbf{arg}(z)\). Het argument is tot op gehele veelvouden van \(2\pi\) na bepaald. Je kunt voor elk complex getal dus wel een hoek vinden in het interval \((-\pi,\pi]\). Deze waarde, groter dan \(-\pi\) en kleiner dan of gelijk aan \(\pi\), heet wel de hoofdwaarde van het argument van \(z\) en noteren we als \(\mathbf{Arg}(z)\).

Bereken exact de hoofdwaarde van het argument van het complexe getal \(z=-\tfrac{1}{2}-\tfrac{1}{2}\!\sqrt{3}\,\mathrm{i}\).

Als \[z=-\tfrac{1}{2}-\tfrac{1}{2}\!\sqrt{3}\,\mathrm{i}\] dan \[z=\cos(-\tfrac{2}{3}\!\pi) + \mathrm{i}\sin(-\tfrac{2}{3}\!\pi)\] en hebben we te maken met de volgende situatie in het complexe vlak:

Dus: \[\begin{aligned} \mathrm{arg}(z)&=-\tfrac{2}{3}\!\pi+2k\pi\quad \text{voor gehele getallen }k\\ \mathrm{Arg}(z)&=-\tfrac{2}{3}\!\pi\end{aligned}\]

Nieuw voorbeeld

Met de rekenregels voor goniometrische functies kunnen we nu uitzoeken hoe vermenigvuldiging van twee complexe getallen op de eenheidscirkel leidt tot een nieuw complex getal op de eenheidscirkel en een formule voor dit product afleiden.

Het product van twee getallen \(z_1\) en \(z_2\) op de eenheidscirkel is weer een getal op de eenheidscirkel, en wel het getal waarvan het argument gelijk is aan de som van de argumenten van \(z_1\) en \(z_2\).

In formuletaal:
Als \[z_1=\cos\varphi_1 + \mathrm{i} \sin\varphi_1\qquad\text{en}\qquad z_2=\cos\varphi_2 + \mathrm{i} \sin\varphi_2\] dan \[z_1z_2=\cos(\varphi_1+\varphi_2) + \mathrm{i} \sin(\varphi_1+\varphi_2)\]

Als \[z_1=\cos\varphi_1 + \mathrm{i} \sin\varphi_1\qquad\text{en}\qquad z_2=\cos\varphi_2 + \mathrm{i} \sin\varphi_2\] dan \[\begin{aligned}z_1z_2&= \bigl(\cos\varphi_1 + \mathrm{i} \sin\varphi_1\bigr)\bigl(\cos\varphi_2 + \mathrm{i} \sin\varphi_2\bigr) \\ \\ &= \bigl(\cos\varphi_1\cos\varphi_2 - \sin\varphi_1\sin\varphi_1\bigr)+\mathrm{i}\bigl(\cos\varphi_1\sin\varphi_2+\sin\varphi_1\cos\varphi_2\bigr)\\ \\ &= \cos(\varphi_1+\varphi_2) + \mathrm{i} \sin(\varphi_1+\varphi_2) \end{aligned}\] De eerste stap is enkel haakjes wegwerken en de tweede stap is toepassing van de volgende goniometrische rekenregels \[\begin{aligned} \cos(\varphi_1+\varphi_2)&=\cos\varphi_1\cos\varphi_2 - \sin\varphi_1\sin\varphi_1\\ \\ \sin(\varphi_1+\varphi_2)&= \cos\varphi_1\sin\varphi_2+\sin\varphi_1\cos\varphi_2\end{aligned}\]

Voor het quotiënt van complexe getallen op de eenheidscirkel geldt:

Het quotiënt \(\dfrac{z_1}{z_2}\) van twee getallen op de eenheidscirkel is weer een getal op de eenheidscirkel, en wel het getal waarvan het argument gelijk is aan het verschil van de argumenten van \(z_1\) en \(z_2\).

In formuletaal:
Als \[z_1=\cos\varphi_1 + \mathrm{i} \sin\varphi_1\qquad\text{en}\qquad z_2=\cos\varphi_2 + \mathrm{i} \sin\varphi_2\] dan \[\frac{z_1}{z_2}=\cos(\varphi_1-\varphi_2) + \mathrm{i} \sin(\varphi_1-\varphi_2)\]