Poolcoördinaten

Complexe getallen: Het complexe vlak

Poolcoördinaten

Elk complex getal $z=x+\mathrm{i}\,y$ ongelijk aan $0$ is te schrijven in de vorm

$z = r\,(\cos\varphi+\mathrm{i}\,\sin\varphi)$ met

$r=|z|=\sqrt{x^2+y^2}\quad\text{en}\quad \varphi=\arg(z)$ Merk op dat $r$ de modulus of absolute waarde van het complexe getal is en dat we de hoek $\varphi$ het argument van $z$ noemen, net als bij complexe getallen op de eenheidscirkel. Er geldt $x=r\,\cos\varphi$ en $y=r\,\sin\varphi$ . We spreken van poolcoördinaten $[r,\varphi]$ .

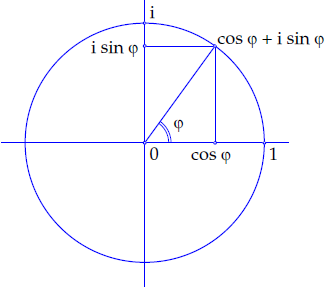
poolcoordinaten

Bekijk een complex getal $z=x+\mathrm{i}\,y$ ongelijk aan $0$ dat te schrijven is in de vorm $z = r\,(\cos\varphi+\mathrm{i}\,\sin\varphi)$ . Voor het verband tussen $x$ , $y$ , $r$ en $\varphi$ geldt in het algemeen:

$\begin{aligned}x=r\,\cos\varphi &,\quad y=r\,\sin\varphi\\ r=\sqrt{x^2+y^2} &,\quad \tan\varphi=\frac{y}{x}\end{aligned}$ Vaak concludeert men dat de waarde van het argument gegeven wordt door de formule

$\arg(z)=\arctan \left(\frac{\mathrm{Im}(z)}{\mathrm{Re}(z)}\right)\tiny.$ Dit is alleen waar als $\mathrm{Re}(z)\gt 0$ en in andere gevallen niet (ga dit zelf na aan de hand van het complexe getal $-1-\mathrm{i}$ ).

Verder is het argument alleen maar modulo $2\pi$ bepaald. In de praktijk volstaan bovenstaande vergelijkingen om $\varphi$ te bepalen, maar er liggen dus een paar addertjes onder het gras. Als $x=y=0$ , dan is $\varphi$ niet gedefinieerd. Als $x=0, y>0$ , dan is $\varphi =\tfrac{1}{2}\!\pi$ , en als $x=0, y<0$ , dan is $\varphi =-\tfrac{1}{2}\!\pi$ . In alle andere gevallen, kun je $\varphi$ wel berekenen met behulp van de arctangens (inverse functie van de tangens), maar moet je er dan wel rekenen mee houden dat de artangens altijd een getal tussen $-\tfrac{1}{2}\!\pi$ en $\tfrac{1}{2}\!\pi$ oplevert. Als $x<0$ , dat wil zeggen als het complexe getal een negatief reëel deel heeft, dan moet je bij het resultaat van $\arctan\left(\dfrac{y}{x}\right)$ nog $\pi$ bij optellen of aftrekken.

Samenvattend hebben we dus:

$\begin{aligned}\text{als } x=0, y>0\;&\text{dan }\varphi=\tfrac{1}{2}\!\pi+2k\pi\\ \text{als } x=0, y<0\;&\text{dan }\varphi=-\tfrac{1}{2}\!\pi+2k\pi\\ \text{als } x<0, y>0\;&\text{dan }\varphi=\arctan\left(\dfrac{y}{x}\right)+\pi+2k\pi\\ \text{als } x<0, y<0\;&\text{dan }\varphi=\arctan\left(\dfrac{y}{x}\right)-\pi+2k\pi\\ \text{als } x>0\;&\text{dan }\varphi=\arctan\left(\dfrac{y}{x}\right)+2k\pi\end{aligned}$ voor een zeker geheel getal $k$ , omdat het argument enkel op gehele veelvouden van $2\pi$ na bepaald is. We kunnen altijd het hoofddeel in het interval $(-\pi,\pi]$ kiezen; we spreken dan weer van de hoofdwaarde van het argument en noteren dit, net als bij complexe getallen op de eenheidscirkel, met $\mathbf{Arg}(z)$ . In bovenstaande formulering hebben we deze formules zodanig opgeschreven dat de hoofdwaarde verkregen wordt door de modulo-term met het veelvould van $2\pi$ weg te laten.

Voor de hoofdwaarde van het argument van een complex getal $z$ is ook de volgende meer ingewikkelde, moeilijk te onthouden formule te gebruiken, zonder dat je in het geval van een complex getal met negatief reëel deel een arctangens-waarde hoeft aan te passen:

$\mathrm{Arg}(z)=\begin{cases}\pi&\text{als } z\text{ op de negatieve reële as ligt}\\ 2\arctan\left(\dfrac{\mathrm{Im}(z)}{|z|+\mathrm{Re} (z)}\right)&\text{anders }\end{cases}$

Voor de liefhebber geven nog een bewijs van de uitspraak dat $\mathrm{Arg}(z)=2\arctan\left(\dfrac{\mathrm{Im}(z)}{|z|+\mathrm{Re} (z)}\right)$ als $z$ niet op de negatieve reële as ligt. We maken daarbij gebruik van de formule

$\tan\left(\frac{\alpha}{2}\right)=\dfrac{\sin(\alpha)}{1+\cos(\alpha)}\tiny.$ Deze laatste formule volgt uit de verdubbelingsformules voor goniometrische functies:

$\begin{aligned}\tan\left(\frac{\alpha}{2}\right)&=\dfrac{\sin\left(\dfrac{\alpha}{2}\right)}{\cos\left(\dfrac{\alpha}{2}\right)}\\ &\phantom{uvwxyz}\color{blue}{\text{definitie tangens}}\\ &=\dfrac{2\sin\left(\dfrac{\alpha}{2}\right)\cdot\cos\left(\dfrac{\alpha}{2}\right)}{2\cos^2\left(\dfrac{\alpha}{2}\right)}\\ &\phantom{uvwxyz}\color{blue}{\text{teller en noemer vermenigvuldigd met }2\cos\left(\frac{\alpha}{2}\right)}\\ &=\dfrac{\sin\left({\alpha}\right)}{1+\cos\left(\alpha\right)}\\ &\phantom{uvwxyz}\color{blue}{\cos(2x) =2\cos(x)^2-1\text{ en }\sin(2x)=2\sin(x)\cdot\cos(x)}\\ \end{aligned}$

$\varphi=\arg(z)$ wordt bepaald door de voorwaarden

$\begin{aligned}\cos(\varphi)&=\dfrac{\mathrm{Re}(z)}{|z|}\\ \sin(\varphi)&=\dfrac{\mathrm{Im}(z)}{|z|}\\ \varphi&\in (-\pi,\pi]\tiny.\end{aligned}$ Uit de eerste twee voorwaarden volgt

$\tan\left(\frac{\varphi}{2}\right)=\frac{\sin(\varphi)}{1+\cos(\varphi)}=\dfrac{ \dfrac{\mathrm{Im}(z)}{|z|} }{1+\dfrac{\mathrm{Re}(z)}{|z|}}=\dfrac{\mathrm{Im}(z)}{|z|+\mathrm{Re}(z)}\tiny.$ Uit de derde voorwaarde volgt $\dfrac{\varphi}{2}\in(-\pi,\pi]$ .

Volgens de theorie over inverse goniometrische functies is de functie $\arctan$ de inverse van $\tan$ op $-\tfrac{1}{2}\pi,\tfrac{1}{2}\pi]$ . Daarom geldt voor $\varphi\ne\pi$ , dat wil zeggen voor $z$ niet op de negatieve reële as:

$\varphi = 2\arctan\left(\tan\left(\dfrac{\varphi}{2}\right)\right)=2\arctan\left(\dfrac{\Im(z)}{|z|+\Re(z)}\right)\tiny.$

Rekenschema voor hoofdargument De kwadranten van het complexe vlak zijn in onderstaande figuur genummerd.

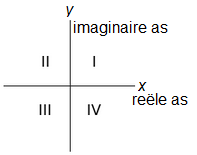
Onderstaand rekenschema's geven aan hoe de hoofdwaarde $\mathrm{Arg}(z)$ van het complexe getal $z=x+y\,\ii$ berekend kan worden aan de hand van de positie van het corresponderende punt $(x,y)$ in het complexe vlak.

$\begin{array}{|c|c|c|} \hline \textit{Kwadrant} & \textit{Teken van }x\textit{ en }y & \mathrm{Arg}(z)\\ \hline\hline \mathrm{I} & x>0,\quad y>0 & \arctan(y/x) \\ \hline \mathrm{II} & x<0,\quad y>0 & \pi+\arctan(y/x) \\ \hline \mathrm{III} & x<0,\quad y<0 & -\pi+ \arctan(y/x)\\ \hline \mathrm{IV} & x>0,\quad y<0 & \arctan(y/x) \\ \hline \end{array}$ Voor punten op de randen van de kwadranten kun je het volgende schema hanteren.

$\begin{array}{|c|c|c|c|} \hline \textit{Rand} & \textit{type van complex getal }z & \textit{condities voor }x\text{ en }y & \mathrm{Arg}(z)\\ \hline\hline \mathrm{IV/I} & \text{reëel en positief} & x>0,\quad y=0 & 0 \\ \hline \mathrm{I/II} & \text{zuiver imaginair met Im}(z)>0 & x=0,\quad y>0 & \tfrac{1}{2}\pi \\ \hline \mathrm{II/III} & \text{reëel en positief} & x<0,\quad y=0 & \pi\\ \hline \mathrm{III/IV} & \text{zuiver imaginair met Im}(z)<0 & x=0,\quad y<0 & -\tfrac{1}{2}\pi\\ \hline \text{oorsprong} & \text{nul} & x=0,\quad y=0 & \text{onbepaald} \\ \hline \end{array}$

De notatie met imaginaire $e$ -machten geeft

$z=r\,e^{\,\mathrm{i}\,\varphi}$ Men noemt dit wel de polaire vorm van het complexe getal $z$ .

$\phantom{x}$

Bekijk voldoende voorbeelden van conversies tussen standaardvorm en polaire vorm van een complex getal.

Bereken exact de poolcoördinaten van het complexe getal $z=-\mathrm{i}$ .
Geef hierbij de hoofdwaarde.

$\rv{r,\varphi}=\rv{1,-\tfrac{1}{2}\pi}$

De $r$ -coördinaat is gelijk aan de absolute waarde van $z$ ; om deze waarde te berekenen hoef je alleen het reële en imaginaire deel van $z$ te bepalen:

$\begin{aligned}\mathrm{Re}(z)&= 0\\ \mathrm{Im}(z)&= -1\\ \\ r&=|z|\\ &= \sqrt{\bigl(\mathrm{Re}(z)\bigr)^2+\bigl(\mathrm{Im}(z)\bigr)^2} \\ &=\sqrt{\bigl(0\bigr)^2+\bigl(-1\bigr)^2}\\ &=1\end{aligned}$ Het argument van $z$ , genoteerd als $\varphi$ , haal je uit de volgende twee vergelijkingen:

$\cos(\varphi)= \frac{\mathrm{Re}(z)}{r}\qquad\mathrm{en}\qquad \sin(\varphi)= \frac{\mathrm{Im}(z)}{r}$ In dit geval:

$\cos(\varphi)= \frac{0}{1}=0\qquad\mathrm{en}\qquad \sin(\varphi)= \frac{-1}{1}=-1$ Uit de laatste twee vergelijkingen en de positie van het complexe getal in het complexe vlak leidt je de hoofdwaarde van het argument af:

$\varphi=-\tfrac{1}{2}\pi$

Zie onderstaande figuur voor een meetkundige interpretatie van de overgang van de standaardvorm van een complex getal naar die van poolcoördinaten. Het complexe getal is blauw getekend. De absolute waarde $r$ en het argument $\varphi$ ervan zijn rood getekend.

Nieuw voorbeeld

Het argument van een complex getal kunnen we gebruiken om rechte lijnen in het vlak via complexe getallen te beschrijven. Dit gaat als volgt. Stel $\varphi$ is een reëel getal en $w=a+b\,\mathrm{i}$ een willekeurig gekozen complex getal met reëel deel $a$ en imaginair deel $b$ . Dan wordt de lijn door het punt $\rv{a,b}$ met richtingscoëfficiënt $\tan(\varphi)$ niet alleen gegeven door de vergelijking

$\sin(\varphi)\cdot (x-a)-\cos(\varphi)\cdot (y-a)=0$ maar ook door de volgende complexe vergelijking (met onbekende $z$ ):

$\arg(z-w) = \varphi\quad (\text{mod }\pi)$

Mathcentre videos

Modulus and Argument (11:02)

Polar Form (11:29)