Complexe getallen: Complexe machten, wortels en veeltermen
 Complexe derdemachtswortels
Complexe derdemachtswortels
We weten al dat complexe vierkantswortels bestaan, maar we kunnen nog een stap verder gaan en de derdemachtswortels introduceren. Eerst maar weer een voorbeeld.
Complexe derdemachtswortel van -1 Wat zou \(\sqrt[3]{-1}\) kunnen zijn? We willen de vergelijking \[z^3=-1\] in de verzameling van complexe getallen oplossen. Daarvoor schrijven we eerst \(-1\) in polaire vorm: \[-1 = e^{\pi\,\mathrm{i}+2\,k\,\pi\,\mathrm{i}}\] voor gehele getallen \(k\). We schrijven \(z\) ook in polaire vorm, zeg \[z=r\, e^{\,\mathrm{i}\,\varphi}\] Dan geldt: \[z^3=r^3\, e^{\,\mathrm{i}\,3\varphi}\] We moeten dus reële getallen \(r>0\) en \(\varphi\) in het interval \((-\pi, \pi]\) vinden zodanig dat \[r^3=1\qquad\text{en}\qquad 3\varphi=\pi+2k\pi\] Zonder de inperking van \(\varphi\) tot het interval \((-\pi, \pi]\) vinden we \[r=1\quad\text{en}\quad \varphi=\tfrac{1}{3}\pi+\tfrac{2}{3}k\,\pi\] met gehele getallen \(k\). De oplossingen binnen de beperking van \(\varphi\) zijn dus: \[[r=1,\phi= \tfrac{1}{3}\pi]\quad\text{of}\quad [r=1,\varphi= \pi]\quad\text{of}\quad [r=1,\varphi= -\tfrac{1}{3}\pi]\] In polaire vorm hebben we complexe oplossingen voor de vergelijking \(z^3=-1\) gevonden; we kunnen ze ook opschrijven als: \[z=e^{(\tfrac{1}{3}\pi+\!\tfrac{2}{3}k\,\pi)\,\mathrm{i}}\quad\text{voor }k=0, 1, 2\] Voor andere gehele waarden van \(k\) krijgen we vanwege de periodiciteit van de complexe exponentiële functie steeds één van de genoemde complexe wortels. In standaardvorm hebben we de volgende oplossingen: \[z=\cos\bigl(\tfrac{1}{3}\pi+\tfrac{2}{3}k\,\pi\bigr)+ \cos\bigl(\tfrac{1}{3}\pi+\tfrac{2}{3}k\,\pi\bigr)\mathrm{i}\quad\text{voor }k=0, 1, 2\] Voor \(k=1\) hebben we een reëele oplossing \(-1\). Als hoofdwaarde van \(\sqrt[3]{-1}\) kiezen we in dit geval \(k=0\) en dus de oplossing \(z=e^{\tfrac{1}{3}\pi\,\mathrm{i}}=\tfrac{1}{2}+\mathrm{i}\,\tfrac{1}{2}\sqrt{3}\).
Het volgende plaatje laat zien waar de oplossingen zich op de eenheidscirkel bevinden:
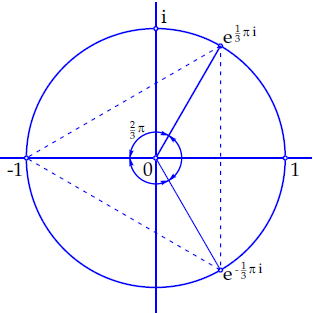
De punten die corresponderen met de complexe 3-demachtswortels van \(-1\) vormen de hoekpunten van een gelijkzijdige driehoek met de oorsprong als centrum. De voerstralen van de drie 3-demachtswortels van \(-1\) maken onderling hoeken van \(\tfrac{2}{3}\pi\).
Het algemene geval gaat net zo.
De complexe derdemachtswortelfunctie Voor een willekeurige getal \(z\) kunnen we de complexe derdemachtswortelfunctie in polaire vorm definiëren: \[\begin{aligned}\sqrt[3]{z}&=\sqrt[3]{|z|}\cdot e^{\,\mathrm{i}\tfrac{1}{3}\mathrm{arg}(z)}\\ \\ \text{hoofdtak van }\sqrt[3]{z}&=\sqrt[3]{|z|}\cdot e^{\,\mathrm{i}\tfrac{1}{3}\mathrm{Arg}(z)}\end{aligned}\] In termen van de complexe exponentiële functie en complexe logaritme kunnen we de complexe wortelfunctie gewoonweg definiëren als \[\sqrt[3]{z}=e^{\tfrac{1}{3}\ln(z)}\]
Dus, als \(z=r\cdot e^{\,\mathrm{i}\,\varphi}\), met \(r>0\) en \(-\pi<\varphi\le\pi\), dan is de hoofdwaarde van \(\sqrt[3]{z}\) gelijk aan \(\sqrt[3]{r}\cdot e^{\,\mathrm{i}\tfrac{1}{3}\varphi}\).
Wanneer je de vergelijking \(z^3=1\) in \(\mathbb{C}\) wilt oplossen, kun je de oplossing best als \(z=\sqrt[3]{1}\) opschrijven, als je maar bedenkt dat hiermee eigenlijk de volgende drie oplossingen genoteerd worden: \(z=e^{0\,\ii}=1\), \(z=e^{\tfrac{2}{3}\pi\,\ii}=-\tfrac{1}{2}+\tfrac{1}{2}\sqrt{3}\,\ii\) en \(z=e^{\tfrac{4}{3}\pi\,\ii}=-\tfrac{1}{2}-\tfrac{1}{2}\sqrt{3}\,\ii\). Immers, \(\arg(1)=2k\pi\ii\) voor gehele getallen \(k\).


