Complexe getallen: Complexe machten, wortels en veeltermen
 Complexe n-demachtswortels
Complexe n-demachtswortels
We weten al dat complexe vierkantswortels en derdemachtswortels bestaan en dan is de stap naar \(n\)-demachtswortels met \(n\gt 3\) niet zo groot meer. Het algemene geval gaat namelijk op dezelfde manier.
Stel \(n\) is een natuurlijk getal groter of gelijk aan 2.
Elk complex getal \(z=r\cdot e^{\,\mathrm{i}\,\varphi}\) met \(r=|z|>0\) en \(-\pi<\varphi\le\pi\) heeft precies \(n\) \(n\)-demachtswortels, namelijk \[\sqrt[n]{z}=r^\tfrac{1}{n}\cdot e^{(\tfrac{1}{n}\varphi+\tfrac{2}{n}k\,\pi)\,\mathrm{i}}\quad\text{voor }k=0,1,\ldots,n-1\]
De complexe n-demachtswortelfunctie Voor een willekeurige getal \(z\) kunnen we de complexe \(n\)-demachtswortelfunctie in polaire vorm definiëren: \[\begin{aligned}\sqrt[n]{z}&=\sqrt[n]{|z|}\cdot e^{\,\mathrm{i}\tfrac{1}{n}\mathrm{arg}(z)}\\ \\ \text{hoofdtak van }\sqrt[n]{z}&=\sqrt[n]{|z|}\cdot e^{\,\mathrm{i}\tfrac{1}{n}\mathrm{Arg}(z)}\end{aligned}\] In termen van de complexe exponentiële functie en logaritme kunnen we de complexe wortelfunctie gewoonweg definiëren als \[\sqrt[n]{z}=e^{\tfrac{1}{n}\ln(z)}\]
Dus, als \(z=r\cdot e^{\,\mathrm{i}\,\varphi}\), met \(r>0\) en \(-\pi<\varphi\le\pi\), dan is de hoofdwaarde van \(\sqrt[n]{z}=\sqrt[n]{r}\cdot e^{\,\mathrm{i}\tfrac{1}{n}\varphi}\).
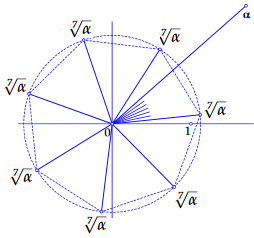
Hieronder zijn de zeven 7-demachtswortels \(\sqrt[7]{\alpha}\) getekend voor \(\alpha=1.7+1.5\,\ii\).
Hiervoor geldt: \[\begin{aligned}|\alpha|&=\sqrt{1.7^2+1.5^2}\approx 2.267\\ \arg(\alpha)&=\arctan\bigl(\frac{1.5}{1.7}\bigr)+2k\pi\approx 0.723+2k\pi\quad\text{voor gehele getallen }k\tiny.\end{aligned}\] Dus: \[\begin{aligned}\left|\sqrt[7]{\alpha}\right|&=\sqrt[7]{\left|\alpha\right|}\approx 1.124\\ \arg(\sqrt[7]{\alpha})&=\tfrac{1}{7}\arg(\alpha)\approx 0.103+\tfrac{2k\pi}{7}\quad\text{voor }k=0,1,\dots 6\tiny.\end{aligned}\] Samengevat: \[\sqrt[7]{1.7+1.5\,\ii}\approx 1.124\,e^{(0.103+\frac{2k\pi}{7})\,\ii}\quad\text{voor }k=0,1,\dots 6\tiny.\] Alle getekende wortels maken even veel aanspraak op de notatie \(\sqrt[7]{\alpha}\), maar in het eerste kwadrant van het complexe vlak is een speciale wortel (het dichtst liggend bij \(1\)) die we de hoofdwaarde van de 7-demachtswortel noemen.