The Goldman-Hodgkin-Katz voltage equation

Bioelectricity: Electric model of the cell membrane

The Goldman-Hodgkin-Katz voltage equation

We have already seen how the resting membrane potential of two ion species and ion channels can be described as a weighted sum of the Nernst potentials of the of ions. The weighting depended on the relative conductivities of the ionic species. Such a formula can be written down for several ion species, for example, for the main monovalent ions (potassium, sodium, chloride)

The linearized GHK equation for 3 ion channels The linearized GHK equation for the most important monovalent ions (potassium, sodium, chloride) is as follows: \[V_m=\frac{g_\mathrm{K}E_\mathrm{K}+g_\mathrm{Na}E_\mathrm{Na}+g_\mathrm{Cl}E_\mathrm{Cl}}{g_\mathrm{K}+g_\mathrm{Na}+g_\mathrm{Cl}}\]

But the situation is actually more complicated because the conductivity of an ion depends on the concentration of the ion. A better measure is permeability. For the main monovalent ions (potassium, sodium, chloride) in the cell, you get the following equation, known as the Goldman-Hodgkin-Katz equation or simply as the GHK equation

The GHK equation \[\begin{aligned} V_m&=-\frac{RT}{F}\cdot \log_{10}\left(\frac{P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{i}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{i}+P_\mathrm{Cl}[\mathrm{Cl}^{-}]_\mathrm{e}}{P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{e}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{e}+P_\mathrm{Cl}[\mathrm{Cl}^{-}]_\mathrm{i}}\right)\\ \\ &= \frac{RT}{F}\cdot \log_{10}\left(\frac{P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{e}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{e}+P_\mathrm{Cl}[\mathrm{Cl}^{-}]_\mathrm{i}}{P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{i}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{i}+P_\mathrm{Cl}[\mathrm{Cl}^{-}]_\mathrm{e}}\right)\end{aligned}\] where the \(P\)'s stand for the permeability of the membrane for the specific ion, and the ion concentrations both within (index "i") and outside (index "e") are given.

Note that the negative valence of the chloride ion has already been included in the GHK equation by exchanging the interior and exterior concentration in the numerator and denominator relative to the potassium and sodium ion. In other words, we have applied the calculation rule \(-\log\left(\frac{A}{B}\right)=\log\left(\frac{B}{A}\right)\).

In order to calculate the resting membrane potential using the GHK equation we only need to know the ratio of ion permeability.

At a temperature of \(29.25\;{}^{\circ}\mathrm{C}\) the formula for the membrane voltage in mV is: \[V_m= 60 \cdot \log_{10}\left(\frac{P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{e}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{e}+P_\mathrm{Cl}[\mathrm{Cl}^{-}]_\mathrm{i}}{P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{i}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{i}+P_\mathrm{Cl}[\mathrm{Cl}^{-}]_\mathrm{e}}\right)\]

For those who are wondering how the GHK voltage equation looks like when also the calcium ion (\(\mathrm{Ca}^{2+}\) ) is taken into account in the discussion: the formulas are more complex (see below for the calculation), but the effect of calcium in the physiological situation of a cell at rest is in practice so low that you're usually better off to leave it out. The calculation is as follows: \[V_m=\frac{RT}{F}\cdot\log_{10}(y)\] where \(\displaystyle y=\frac{-b+\sqrt{b^2-4ac}}{2a}\) is the zero of the quadratic equation \[ay^2+by+c=0\] for which \[\begin{aligned}a&=4P_\mathrm{Ca}^{2+}[\mathrm{Ca}^{2+}]_\mathrm{i}+P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{i}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{i}+P_\mathrm{Cl}[\mathrm{Cl}^{-}]_\mathrm{e} \\ \\ b&= P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{i}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{i} +P_\mathrm{Cl}[\mathrm{Cl}^{-}]_\mathrm{e}- P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{e}-P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{e}-P_\mathrm{Cl}[\mathrm{Cl}^{-}]_\mathrm{i}\\ \\ c&= -(4P_\mathrm{Ca}^{2+}[\mathrm{Ca}^{2+}]_\mathrm{e}+P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{e}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{e}+P_\mathrm{Cl}[\mathrm{Cl}^{-}]_\mathrm{i})\end{aligned}\] In case \(P_{\mathrm{Ca}^{2+}}=0\) you just get back the previously mentioned GHK equation.

We refer to the previous equation using conductivities as the linearized GHK equation. What we mean by this becomes evident in the following example.

When we limit the GHK equation to only sodium and potassium, then the equation (with reduced \(P_\mathrm{Cl}=0\) ) becomes at a temperature of \(37\;{}^{\circ}\mathrm{C}\) to \[V_m= 61.5 \cdot \log_{10}\left(\frac{P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{e}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{e}}{P_\mathrm{K}[\mathrm{K}^{+}]_\mathrm{i}+P_\mathrm{Na}[\mathrm{Na}^{+}]_\mathrm{i}}\right)\] This can be traced to \[V_m= 61.5 \cdot \log_{10}\left(\frac{[\mathrm{K}^{+}]_\mathrm{e}+\alpha[\mathrm{Na}^{+}]_\mathrm{e}}{[\mathrm{K}^{+}]_\mathrm{i}+\alpha[\mathrm{Na}^{+}]_\mathrm{i}}\right)\] where \(\displaystyle\alpha = \frac{P_\mathrm{Na}}{P_\mathrm{K}}\) (Note: at a temperature of \(29.25\;{}^{\circ}\mathrm{C}\) you should replace \(61.5\) in this formula by \(60\) ).

If \(\alpha=0\), i.e. no permeability of sodium ions, we have the Nernst equation for potassium. When we plot the membrane voltage (mV) then against the logarithm of the potassium concentration outside the cell, we get a straight line with slope equal to 61.5. In the following figure you see, with a logarithmic scale on the horizontal axis, the voltage plotted against potassium concentration outside the cell for various values of \(\alpha\).

V_m versus [K] _outside

It is clear that for small values of \(\alpha\) (and \(\alpha=0.01\) is a realistic value) that the curve is close to the straight-line approximation for a sufficiently high potassium concentration outside the cell. This is what we mean when we say that the linearized GHK equation and the GHK equation lead to almost the same computed voltage.

Let us look at a numerical example for a nerve cell, namely the squid giant axon , at rest at a temperature of \(37\;{}^{\circ}\mathrm{C}\). The table below shows the necessary data and intermediate results. \[
\begin{array}{l|rrrrc}
\mathrm{ion\;} X & [X]_\mathrm{i} & [X]_\mathrm{e} & P_X / P_\mathrm{K} & E_\mathrm{ion}\;(\mathrm{mV}) \\ \hline
\mathrm{K}^{+} & 400 & 20 & 1 & {}-80 \\
\mathrm{Na}^{+} & 50 & 460 & 0.03 & {}+59 \\
\mathrm{Cl}^{-} & 40 & 540 & 0.1 & {}-64 \\
\end{array}\] The resting membrane potential at the given temperature is according to the GHK equation \[V_m=-61.5\cdot \log_{10}\left(\frac{1\times 400+0.03\times 50+0.1\times 540}{1\times 20+0.03\times 460+0.1\times 40}\right)\approx -66.5\;\mathrm{mV}\] When we omit the chloride ions in the calculation, the resting membrane potential \(V_m\) calculated by the GHK equation is not very different; in this case \[V_m=-61.5\cdot \log_{10}\left(\frac{1\times 400+0.03\times 50}{1\times 20+0.03\times 460}\right)\approx -66.1\;\mathrm{mV}\] A similar result is obtained when you assume the ratio of potassium and sodium conductivity equal to 1: 0.1 and use the linearized GHK equation. Then you get namely \[V_m = \frac{1\times -80 + 0.1\times 59}{1+0.1} \approx -67.4\;\mathrm{mV}\]

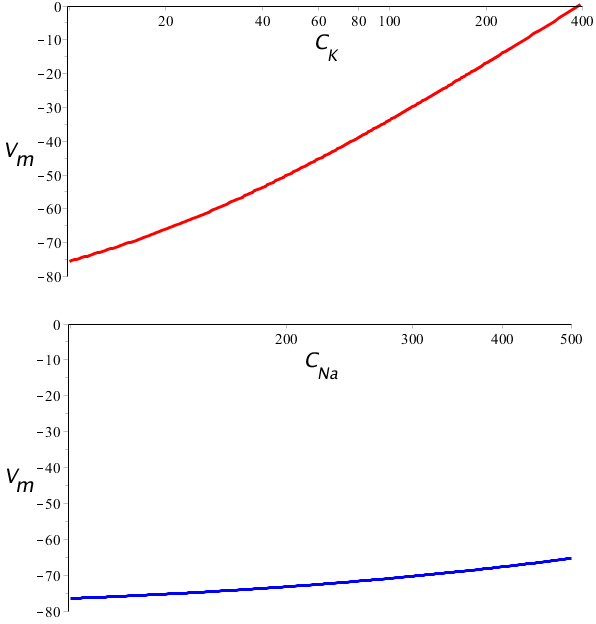
In the graphs below, the resting membrane potential, calculated according to the GHK equation, is plotted against an ion concentration outside the cell, with a logarithmic scale on the horizontal axis. From the graphs can be noticed that a change in potassium concentration outside the cell has a large effect on the resting membrane potential (red graph) and that a change in sodium concentration has a much smaller effect (blue graph). This, of course, is vaused by the differences in permeability of the potassium and sodium ion. The ion with the highest permeability (potassium) is the most important factor of the resting membrane potential, and then the ratio of concentration inside and outside the cell is the most determining factor for the final resting membrane potential. Changes in concentration of other ionic species, such as sodium, have much less effect on the resting membrane potential .