Differentialen en integralen: Toepassingen van integratie
 Lijnintegraal van een functie
Lijnintegraal van een functie
Tot nu toe hebben we een integraal van een functie \(f(x)\) over een interval \([a,b]\) geïnterpreteerd als de oppervlakte onder de grafiek van \(f\). Als toepassing kan je dit in de driedimensionale ruimte bekijken als de totale oppervlakte van een dunne schutting die langs de \(x\)-as staat en op elk punt \((x,0)\) in het \(xy\)-vlak hoogte \(f(x)\) heeft.
Maar waarom zouden we ons beperken tot een kaarsrechte schutting? Kan de schutting niet even goed geplaatst worden langs een kromme \(\mathcal{C}\) in het \(xy\)-vlak? De hoogte moeten we nu beschrijven met een functie in twee variabelen, zeg \(f(x,y)\), waarbij het punt \((x,y)\) steeds op de kromme \(\mathcal{C}\) moet liggen; zie onderstaande figuur.
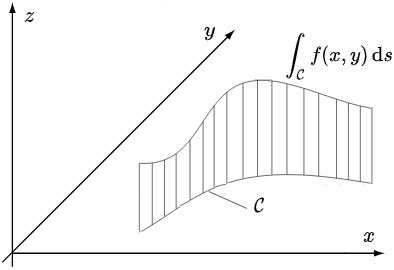
Een tweede consequentie is dat we niet meer de differentiaal \(\dd x\) kunnen gebruiken in het integratieproces. Maar zoals we bij het onderwerp Lengte van een kromme hebben gezien kunnen we ook de lengtetoename \(\dd L\) langs de kromme gebruiken als stukje om de hoogte voor uit te reken. Hiervoor hebben we al wiskundige uitdrukkingen gevonden. Meer gebruikelijk, en ook te zien in bovenstaande figuur, is om de toename in afgelegde weg langs de kromme te gebruiken met het symbool \(\dd s\). Dit is slechts een kleine verandering in taalgebruik en notatie, maar omdat dit in de meeste tekstboeken zo staat nemen we dat in deze theorie pagina overnemen. Gebruikmakend van de Riemann som als benadering van de integraal die we zoeken krijgen we de volgende definities van een lijnintegraal voor een nette functie \(f\), genoteerd als \(\displaystyle\int_\mathcal{C} f\,\dd s\), waarbij \(f\) staat voor \(f(x,y)\) met \((x,y)\) een punt op \(\mathcal{C}\). De kromme \(\mathcal{C}\) wordt ook wel het integratiepad genoemd.
Lijnintegraal van een functie Stel dat \(\mathcal{C}\) een geparametriseerde kromme in het vlak is die beschreven wordt door twee differentieerbare coördinaatfuncties \(x=x(t), y=y(t)\) via een parameter \(t\) in een interval \([a,b]\); we spreken van een gladde kromme. Stel dat \(f(x,y)\) een 'nette' functie is, in ieder geval op \(\mathcal{C}\). Dan is de lijnintegraal van punt \(A=\bigl(x(a),y(a)\bigr)\) naar punt \(B=\bigl(x(b),y(b)\bigr)\) gegeven door \[\int_\mathcal{C}f(x,y)\,\dd s=\int_a^b f\bigl(x(t),y(t)\bigr)\sqrt{\bigl(x'(t)\bigr)^2+\bigl(y'(t)\bigr)^2}\,\dd t\]
\[\begin{aligned}\cv{x(t)\\ y(t)} &= \cv{0 \\ 2}+t\cdot\left(\cv{-2 \\ 1}-\cv{0 \\ 2}\right)\\[0.25cm] &= \cv{0 \\ 2} + t\cdot \cv{-2 \\ -1}\\[0.25cm] &= \cv{-2\,t\\ 2-t}\end{aligned}\] waarbij \(t\in[0,1]\). Langs dit pad kan de lijnintegraal als volgt berekend worden: \[\begin{aligned}\int_C x\,\dd s &= \int_{0}^{1} \bigl(-2\,t\bigr)\sqrt{(-2)^2+(-1)^2}\,\dd t\\[0.25cm] &=\int_{0}^{1} -2\,\sqrt{5}\,t\,\dd t\\[0.25cm] &= \Biggl[-\sqrt{5}\,t^2\Biggr]_{0}^{1}\\[0.25cm] &= -\sqrt{5}-0 \\[0.25cm] &= -\sqrt{5}\end{aligned}\]
Lijnintegraal langs een stuksgewijs gedefinieerde kromme Een lijnintegraal kan ook voor een kromme \(\mathcal{C}\) gedefinieerd worden die bestaat uit aaneengesloten stukjes van gladde krommen, zeg \(\mathcal{C}_1, \mathcal{C}_2, \ldots, \mathcal{C}_n\). De lijnintegraal van een 'nette' functie \(f(x,y)\) over de stuksgewijs gedefinieerde kromme \(\mathcal{C}\) kan dan als volgt berekend worden: \[\int_\mathcal{C}f(x,y)\,\dd s=\int_\mathcal{C_1}f(x,y)\,\dd s + \int_\mathcal{C_2}f(x,y)\,\dd s+ \cdots + \int_\mathcal{C_n}f(x,y)\,\dd s\]
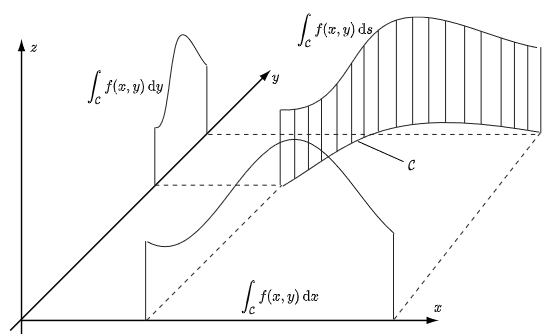
Alternatieve lijnintegralen We hebben in bovenstaande definitie de afgelegde weg \(s\) als variabele voor integratie gebruikt. Dit wordt het meest in toepassingen gebruikt, bijvoorbeeld in klassieke mechanica om de verrichte arbeid om een object langs een bepaalde weg te doen bewegen of om het zwaartepunt van een dunne gebogen staaf te bepalen. Maar in feite kunnen ook andere variabelen zoals \(x\) en \(y\) gebruikt worden als variabele voor integratie. Dan krijg je lijnintegralen van het type \[\int_{\mathcal{C}} f(x,y)\,\dd x\quad\text{en}\quad \int_{\mathcal{C}} f(x,y)\,\dd y\] De lijnintegraal \(\displaystyle \int_{\mathcal{C}} f(x,y)\,\dd s\) stelt de oppervlakte onder het oppervlak \(z=f(x,y)\) maar boven de kromme \(\mathcal{C}\) voor. De integralen \(\displaystyle \int_{\mathcal{C}} f(x,y)\,\dd x\) en \(\displaystyle \int_{\mathcal{C}} f(x,y)\,\dd y\) stellen respectievelijk de oppervlakte van de projectie van dit gebied op het \(xz\)-vlak en het \(yz\)-vlak voor; zie onderstaande figuur:
Ook de combinatie van beide alternatieve lijnintegralen voor twee gladde functies \(f(x,y)\) en \(g(x,y)\) kom je in de praktijk veel tegen: \[\int_{\mathcal{C}}f(x,y)\,\dd x + g(x,y)\,\dd y\] Een voorbeeld: stel dat \(\mathcal{C}\) de kromme \(y=x^2\) van \((0,0)\) naar \((1,1)\) is, dan: \[\begin{aligned}\int_{\mathcal{C}}x^2y\,\dd x + x\,y^2\,\dd y &= \int_{0}^{1} \left(x^2y+\,y^2\,\frac{\dd y}{\dd x}\right)\dd x\\[0.25cm] &= \int_{0}^{1} \left(x^4+2x^6\right)\,\dd x\\[0.25cm] &= \int_{0}^{1} \biggl[\frac{1}{5}x^5+\frac{1}{3}x^6\biggr]_{0}^{1}\\[0.25cm] &= \frac{1}{5}+\frac{1}{3}\\[0.25cm] &= \frac{7}{15}\end{aligned}\] Eigenlijk is er in dit geval geen sprake meer van een lijnintegraal van een functie, maar van een lijnintegraal van een differentiaalvorm. We zullen zien dat er nog meer typen lijnintegralen zijn.
Het begrip lijnintegraal van een functie kan ook tot de driedimensionale ruimte uitgebreid worden.
Lijnintegraal Stel dat \(\mathcal{C}\) een geparametriseerde kromme in de driedimensionale ruimte is die beschreven wordt door drie differentieerbare coördinaatfuncties \(x=x(t), y=y(t), z=z(t)\) via een parameter \(t\) in een interval \([a,b]\). Stel dat \(f(x,y)\) een 'nette' functie is, in ieder geval op \(\mathcal{C}\). Dan is de lijnintegraal tussen de punten \(A=\bigl(x(a),y(a), z(a)\bigr)\) en \(B=\bigl(x(b),y(b), z(b)\bigr)\) gegeven door \[\int_\mathcal{C}f(x,y,z)\,\dd s=\int_a^b f\bigl(x(t),y(t),z(t)\bigr)\sqrt{\bigl(x'(t)\bigr)^2+\bigl(y'(t)\bigr)^2+ \bigl(z'(t)\bigr)^2}\,\dd t\]
\(\bar{z}={}\)\( \dfrac{2\pi}{ \ln(1+2\pi)}-1\)
In feite wordt er gevraagd om de volgende lijnintegraal uit te rekenen: \[\int_{\mathcal{C}} z\cdot \rho(x,y,z)\,\dd s\] Door de parametrisatie hebben we voor de totale massa \(M\) van de staaf: \[\begin{aligned}M &=\int_{\mathcal{C}} \rho(x,y,z)\,\dd s\\[0.25cm] &= \int_{\mathcal{C}} \rho\bigl(x(t),y(t),z(t)\bigr)\cdot \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}\,\dd t\\[0.25cm] &= \int_{0}^{2\pi} \frac{1}{1+t}\sqrt{(-\sin t)^2+\cos^2t+1^2}\,\dd t\\[0.25cm] &= \int_{0}^{2\pi} \frac{1}{1+t} \sqrt{\sin^2t+\cos^2t+1^2}\,\dd t\\[0.25cm] &= \sqrt{2} \int_{0}^{2\pi} \frac{1}{1+t}\,\dd t\\[0.25cm] &= \sqrt{2} \biggl[\ln(1+t)\biggr]_{0}^{2\pi} \\[0.25cm] &= \sqrt{2}\bigl(\ln(1+2\pi)-\ln(1)\bigr)\\[0.25cm] &= \sqrt{2}\ln(1+2\pi)\end{aligned}\] Voor de berekening van de \(z\)-coordinaat van het zwaartepunt hebben we nog het zogenoemde statische moment \(M_{xy}\) nodig. Hierin speelt de dichtheidsfunctie de rol van een weegfactor in de integratie van de verticale coördinaat langs de spiraal: \[\begin{aligned}M_{xy} &= \int_{\mathcal{C}} z\cdot \rho(x,y,z)\,\dd s\\[0.25cm] &= \int_{\mathcal{C}} z\cdot \rho\bigl(x(t),y(t,)z(t)\bigr)\cdot \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}\,\dd t\\[0.25cm] &= \int_{0}^{2\pi}t\cdot \frac{1}{1+t}\sqrt{(-\sin t)^2+\cos^2t+1^2}\,\dd t\\[0.25cm] &= \int_{0}^{2\pi}t\cdot \frac{1}{1+t}\sqrt{\sin^2t+\cos^2t+1^2}\\[0.25cm] &= \sqrt{2}\int_{0}^{2\pi}\frac{t}{1+t}\,\dd t\\[0.25cm] &= \sqrt{2}\int_{0}^{2\pi}\left(1-\frac{1}{1+t}\right)\dd t\\[0.25cm] &= \sqrt{2}\cdot \biggl[t-\ln(1+t)\biggr]_{0}^{2\pi} \\[0.25cm] &= \sqrt{2}\Bigl(\bigl(2\pi-\ln(1+2\pi)\bigr)-\bigl(0-\ln(1)\bigr)\Bigr)\\[0.25cm] &= \sqrt{2}\bigl(2\pi-\ln(1+2\pi)\bigr)\end{aligned}\]
De verticale coördinaat \(\bar{z}\) van het zwaartepunt is dan: \[\begin{aligned}\bar{z} &= \frac{M_{xy}}{M} \\[0.25cm] &= \frac{\sqrt{2}\bigl(2\pi-\ln(1+2\pi)\bigr)}{ \sqrt{2}\ln(1+2\pi)}\\[0.25cm] &= \frac{2\pi}{ \ln(1+2\pi)}-1\\[0.25cm] &\approx 2.164 \end{aligned}\] De benadering van het exaxte resultaat laat zien dat de verticale coordinaat van het zwaartepunt kleiner is dan de waarde \(\pi\) bij een spiraal met constante dichtheid. Dit klopt met de verwachting dat het zwaartepunt lager ligt bij een dichtheid die afneemt met de hoogte.


