De halveringsmethode, ook wel de methode van bisectie (Latijn voor tweedeling) of binair zoeken genaamd, is een speciaal geval van een methode waarbinnen het zoekgebied voor een nulpunt in stappen systematisch verkleind wordt.

We beginnen met een continue functie \(f(x)\) op het gesloten interval \([a,b]\) met \(f(a)\cdot f(b)<0\).
Met andere woorden, \(f(a)\) en \(f(b)\) hebben verschillend teken en continuïteit betekent zoveel als dat je de grafiek van \(f\) op \([a,b]\) kunt tekenen zonder de pen van het papier af te hoeven halen. Dan geldt de tussenwaardestelling die zegt dat er minstens een nulpunt van \(f\) op het open interval \((a,b)\) te vinden is.

Het enige wat ons te doen staat is het interval waarin we een nulpunt zoeken systematisch te verkleinen. In de halveringsmethode gebeurt dit —nomen est omen— door herhaald deelintervallen van \([a,b]\) te halveren en in elke stap te bepalen in welk interval zich op zijn minst één nulpunt bevindt.

Aan het begin is het interval gelijk aan \([a,b]\) en onderzoek je eerst of het getal \(p_1=\tfrac{a+b}{2}\) een nulpunt van de functie \(f\) is. Als dit het geval is ben je klaar omdat een nulpunt gevonden is; zo niet, dan splits je het interval in een linker- en rechterdeel, \([a,p_1]\) respectievelijk \([p_1,b]\). Met welk interval de zoektocht naar een nulpunt verder gaat hangt af van het teken van \(f(p_1)\). Als dit teken tegengesteld is aan dat van \(f(a)\) kies je het linkerinterval en anders ga je verder met het rechterinterval. Dit halveringsproces herhaal je net zolang totdat je op een nulpunt gestuit bent óf de helft van de lengte van het interval kleiner is dan een vooraf gekozen waarde. In het laatste geval kies je als antwoord het midden van het laatst gevonden interval als benadering van het nulpunt van de functie. Onderstaande figuur illustreert de eerste iteraties in de halveringsmethode om een nulpunt \(p\) van een functie \(f\) te vinden.

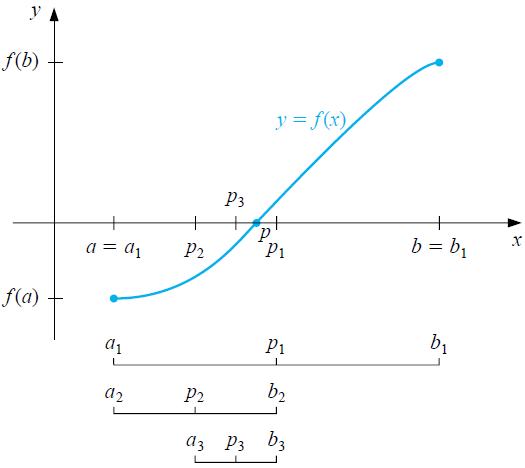
Wat je dus krijgt is een rijtje intervallen \[[a_1,b_1], [a_2,b_2], [a_3,b_3], \ldots\] en een rijtje benaderingen van een nulpunt \[p_1, p_2, p_3, \ldots \] met \(a_1,a_2,a_3,\ldots\) een stijgend rijtje getallen beginnend bij \(a_1=a\), en \(b_1,b_2,b_3,\ldots\) een dalend rijtje getallen beginnend bij \(b_1=b\) zodanig dat \[|b_1-a_1|, |b_2-a_2|, |b_3-a_3|, \ldots\] een strikt dalend rijtje van nietnegatieve reële getallen is. Volgens bovenstaand voorschrift stoppen we zodra (toevalligerwijs) een nulpunt gevonden is (\(f(p_n)=0\) voor zekere \(n\)), óf na \(n\) stappen als \[\left|\frac{b_n-a_n}{2}\right|<\epsilon\] voor een vooraf gekozen tolerantie \(\epsilon\). Met andere woorden, we stoppen in de halveringsmethode wanneer de afbreekfout kleiner dan de gewenste nauwkeurigheid is.

Er zijn natuurlijk ook andere criteria om te stoppen te bedenken.
Je kan bijvoorbeeld naar de relatieve afbreekfout kijken \[\left|\frac{b_n-a_n}{a_n+b_n}\right|<\epsilon\] of vooraf het aantal iteraties \(n\) instellen op het kleinste natuurlijke getal zodanig dat \[\frac{b-a}{2^n}< \epsilon\tiny.\] In het laatste geval weet je zeker dat de afbreekfout kleiner dan \(\epsilon\) is, maar als je geluk hebt is het resultaat nauwkeuriger. Sowieso is het altijd een goed idee om in een numerieke algoritme het aantal iteraties te begrenzen: dit voorkomt oneindige herhalingslussen.

Het aantal iteraties nodig om een antwoord van een bepaalde nauwkeurigheid te vinden is een maat voor de efficiëntie van de methode. De snelheid waarmee het rijtje benaderingen \(p_1, p_2, \ldots\) dichter bij het nulpunt komt, oftewel convergeert naar het nulpunt, heet de convergentiesnelheid van de methode. De convergentiesnelheid onderzoek je door bij verschillende, steeds kleiner wordende tolerantie na te gaan hoeveel iteraties nodig zijn om de benadering binnen de opgegeven tolerantie te vinden. Meestal gebeurt dit door systematisch de tolerantie te verkleinen volgens een rijtje \(10^{-1}, 10^{-2}, 10^{-3},\ldots \) zodat steeds meer decimalen correct worden. De convergentie is lineair als het verband tussen het aantal iteraties en het aantal correct berekende decimalen lineair is. In de halveringsmethode is dat zo en bovendien geldt bij iedere iteratie dat de afbreekfout halveert.

Verleidelijk is om naar het rijtje \(p_1, p_2, p_3 \ldots\) van middens van de achtereenvolgende intervallen te kijken en één van onderstaande stopcriteria te gebruiken: \[\begin{aligned} |p_n-p_{n-1}| &< \epsilon \\ \\ |f(p_n)| &< \epsilon \\ \\ \left|\frac{p_n-p_{n-1}}{p_n}\right| &< \epsilon\end{aligned}\] Maar elk van deze criteria heeft zo zijn problemen zoals we in opdrachten zullen zien. Bijvoorbeeld, is het mogelijk dat een rijtje \(p_1, p_2, \ldots\) waarden heeft die steeds dichter bij elkaar komen te liggen zonder dat het rijtje zelf dicht bij een vaste waarde uitkomt. Ook vormen kleine functiewaarden helemaal geen garantie dat je dicht bij een nulpunt op het domein van de functie bent.