De halveringsmethode is eenvoudig, maar in het algemeen niet zo efficiënt. Dit komt deels doordat alleen gebruik gemaakt wordt van het teken van de functie in het midden van een (deel)interval en niet van de grootte van de functiewaarde in dit punt. Nuttige informatie die de numerieke methode zou kunnen versnellen negeert men op deze manier. De regula falsi methode, die gebaseerd op lineaire interpolatie op het laatst berekende interval waarbinnen een nulpunt ligt, maakt wel gebruik van deze informatie.

Net als de halveringsmethode begint de regula falsi methode met een interval \([p_0,p_1]=[a,b]\) zodanig dat \(f(a)\cdot f(b)<0\). Maar in deze nieuwe methode wordt niet het midden als hoekpunt van een nieuw interval gekozen maar wordt de functie op \([a,b]\) met een lineaire interpolatiefunctie benaderd en het nulpunt van deze interpolatie gekozen als nieuw hoekpunt. Met ander woorden, de functie wordt eerst benaderd met de koorde tussen de punten \(\bigl(a,f(a)\bigr)\) en \(\bigl(b,f(b)\bigr)\), d.w.z. door de rechte lijn met vergelijking \[y=\frac{f(b)-f(a)}{b-a}\cdot (x-b)+f(b)\tiny.\] Het snijpunt van deze lijn heeft coördinaten \((p_2,0)\) met \[p_2 = b-f(b)\cdot \frac{b-a}{f(b)-f(a)}\tiny.\] Als \(p_2\) een nulpunt van de functie \(f\) is ben je klaar; zo niet, dan splits je het interval in een linker- en rechterdeel, \([a,p_2]\) respectievelijk \([p_2,b]\). Met welk interval de zoektocht naar een nulpunt verder gaat hangt af van het teken van \(f(p_2)\). Als dit teken tegengesteld is aan dat van \(f(a)\) kies je het linkerinterval en anders ga je verder met het rechterinterval. Dit halveringsproces herhaal je net zolang totdat je op een nulpunt gestuit bent óf de verandering in de hoekpunten van het interval kleiner is dan een vooraf gekozen waarde. Merk op dat de intervallen waarin je een nulpunt zoekt niet noodzakelijkerwijs kleinere lengte krijgen. Als antwoord kies je het midden van het laatst gevonden interval als benadering van het nulpunt van de functie. Onderstaande figuur illustreert de eerste iteraties in de halveringsmethode om een nulpunt \(p\) van een functie \(f\) te vinden.

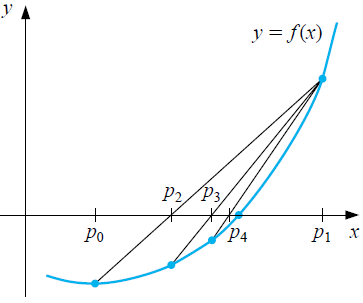
Wat je dus krijgt is een rijtje benaderingen van een nulpunt \[p_0, p_1, p_2, p_3, \ldots \] die steeds dichter bij elkaar komen te liggen. Volgens bovenstaand voorschrift stoppen we zodra (toevalligerwijs) een nulpunt gevonden is (\(f(p_n)=0\) voor zekere \(n\)), óf na \(n\) stappen als \[|p_n-p_{n-1}|<\epsilon\] voor een vooraf gekozen tolerantie \(\epsilon\). Met andere woorden, we stoppen in de regula falsi methode wanneer de afbreekfout kleiner dan de gewenste nauwkeurigheid is.

Een nadeel van de regula falsi methode is dat de benaderingsmethode niet zo snel convergeert als het rijtje \(p_1, p_2, p_3, \ldots\) tot stand komt door steeds weer dezelfde kant van het interval aan te passen zoals in bovenstaande figuur. De regula falsi methode convergeert niet wezenlijk sneller of langzamer dan de halveringsmethode. Maar er zijn slimme aanpassingen bedacht op deze methode die het algoritme wel versnellen; we gaan hier niet op in.