De secant-methode lijkt op de regula falsi methode doordat hierin de functie \(f\) ook in elke iteratiestap lineair geïnterpoleerd wordt. Maar het verschil is dat er geen opsplitsing van een zoekgebied plaats vindt. Sterker nog, het vertrekpunt van de secant-methode hoeft helemaal geen interval te zijn waarbinnen een nulpunt te vinden is.

We beginnen in de secant-methode met twee startwaarden \(p_0=a\) en \(p_1=b\) zodanig dat \(f(p_1)\neq f(p_2)\). Net als in de regula falsi methode wordt de functie eerst benaderd met de koorde tussen de punten \(\bigl(a,f(a)\bigr)\) en \(\bigl(b,f(b)\bigr)\), d.w.z. door de rechte lijn met vergelijking \[y=\frac{f(b)-f(a)}{b-a}\cdot (x-b)+f(b)\tiny.\] Het snijpunt van deze lijn heeft coördinaten \((p_2,0)\) met \[p_2 = b-f(b)\cdot \frac{b-a}{f(b)-f(a)}\tiny.\] Als \(p_2\) een nulpunt van de functie \(f\) is ben je klaar; anders herhaal je dit proces met de twee punten \([p_1, p_2]\). Je krijgt nu een nieuwe benadering via \[p_3 = p_2-f(p_2)\cdot \frac{p_2-p_1}{f(p_2)-f(p_1)}\tiny.\] We rekenen dus met de recursieformule \[p_{n} = p_{n-1}-f(p_{n-1})\cdot \frac{p_{n-1}-p_{n-2}}{f(p_{n-1})-f(p_{n-2})},\quad p_0=a, p_1=b\tiny.\] Onderstaande figuur illustreert de eerste iteraties in de secant-methode om een nulpunt \(p\) van een functie \(f\) te vinden. Ter vergelijking met de regula falsi methode is deze aan de rechterkant toegevoegd voor de getekende situatie; het verschil komt pas na twee iteratiesstappen tevoorschijn.

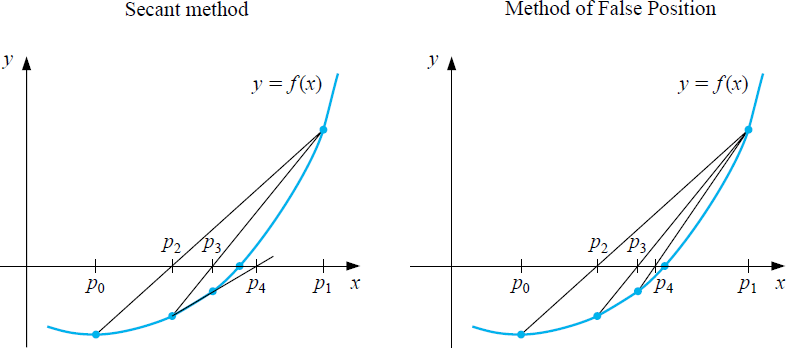
Doordat een nulpunt niet ingeklemd wordt tussen twee waarden in de secant-methode is er geen garantie dat het rijtje \(p_0, p_1, p_2, \ldots\) naar een nulpunt convergeet. Dit is een nadeel, maar "ieder nadeel heb zijn voordeel": de secant-methode werkt sneller dan de regula falsi methode of de halveringsmethode. Hoewel bovenstaande figuur het niet suggereert is de secant-methode efficiënter dan de regula false methode. Dit kunnen we als volgt formeler uitdrukken. Als een rijtje \(p_1, p_2, p3, \ldots\) convergeert naar het nulpunt \(p\) dan is de convergentie van orde \(q\) als er een interval om \(p\) is zodanig dat voor elk begin \(p_1\) in dit interval geldt dat \(|p_{n+1}-p|\le C\cdot |p_n-p|^q\), waarbij \(C<1\) als \(q=1\). We spreken van lineaire convergentie respectievelijk kwadratische convergentie wanneer \(q=1\) respectievelijk \(q=2\). Voor de regula falsi methode kan bewezen worden dat convergentie, net als voor de halveringsmethode, lineair is. Maar voor de secant-methode kan bewezen worden dat \(q\) gelijk is aan de gulden snede \(q=\tfrac{1}{2}(1+\sqrt{5})\approx 1.619\). Dit betekent dat convergentie wezenlijk sneller gaat dan in het lineaire geval.