Operations on sets: intersection, union, difference, and complement

Naive set theory: Elementary notions and notations

Operations on sets: intersection, union, difference, and complement

Sets can be combined in various ways.

Intersection of sets

Intersection

The intersection of two sets \(A\) and \(B\), denoted as \(A\cap B\), is the set of all elements that belong to \(A\) and to \(B\). In formula form: \[A\cap B=\{x \mid x\in A\text{ and } x\in B\}\] We call two sets \(A\) and \(B\) disjoint if \(A\cap B=\emptyset\).

Analogously, the intersection of indexed sets \(X_i\): \[\begin{aligned}\underset{i=1}{\overset{n}{\cap}}X_i&=X_1\cap X_2\cap X_3\cap \cdots\cap X_n\\ \underset{i=1}{\overset{\infty}{\cap}}X_i&=X_1\cap X_2\cap X_3\cap \cdots\end{aligned} \]

Examples

\[\{1,2,3\}\cap \{2,3,4\}=\{2,3\}\] \[[0,\infty)\cap (-1, 1)=[0,1)\] \[\{1,2\}\cap \{3,4\}=\emptyset\] \[\{1,2\}\cap \emptyset=\emptyset\]
If \(X_i=\{x\mid x\in\mathbb{Z}^{+}\text{ and }x\ge i\}\), then \[\begin{aligned}\underset{i=1}{\overset{n}{\cap}}X_i&= \{x\mid x\in\mathbb{Z}^{+}\text{ and }x\ge n\}\\ \underset{i=1}{\overset{\infty}{\cap}}X_i&=\emptyset\end{aligned} \]

The intersection \(A\cap B\) of two sets \(A\) and \(B\) is the largest set that is a subset of both \(A\) and \(B\).

For all sets \(A\), \(B\), and \(C\):

\(\cap\) is idempotent: \(A\cap A= A\).
\(\cap\) is commutative: \(A\cap B= B\cap A\).
\(\cap\) is associative: \(A\cap(B\cap C)= (A\cap B)\cap C\).
\(A\subset B\) if and only if \(A\cap B=A\).
\(A\cap \emptyset=\emptyset\).
\((A\cap B)\subset A\) and \((A\cap B)\subset B\).
If \(A\subset B\) then \((A\cap C)\subset (B\cap C)\).
If \(C\subset A\) and \(C\subset B\) then \(C\subset(A\cap B)\).

The proof follows almost immediately from the definition of the concepts of subset, empty set, and intersection.

Union of sets

Union

The union of two sets \(A\) and \(B\), denoted as \(A\cup B\), is the set of all elements that belong to \(A\) or to \(B\). In formula form: \[A\cup B=\{x \mid x\in A\text{ or } x\in B\}\]

Analogously, the union of indexed sets \(X_i\): \[\begin{aligned}\underset{i=1}{\overset{n}{\cup}}X_i&=X_1\cup X_2\cup X_3\cup \cdots\cup X_n\\ \underset{i=1}{\overset{\infty}{\cup}}X_i&=X_1\cup X_2\cup X_3\cup \cdots\end{aligned} \]

Examples

\[\{1,2,3\}\cup \{2,3,4\}=\{1,2,3,4\}\] \[[0,\infty)\cup (-1, 1)=(-1,\infty)\] \[\{1,2\}\cup \{2\}=\{1,2\}\] \[\{1,2\}\cup \emptyset=\{1,2\}\]
If \(X_i=\{x\mid x\in\mathbb{R}\text{ and }0\lt x\le i\}\), then \[\begin{aligned}\underset{i=1}{\overset{n}{\cup}}X_i&= \{x\mid x\in\mathbb{R}\text{ and }0\lt x\le n\}\\ \underset{i=1}{\overset{\infty}{\cup}}X_i&=\mathbb{R}^{+}\end{aligned} \]

The union \(A\cup B\) of two sets \(A\) and \(B\) is the smallest set of which both \(A\) and \(B\) are subsets.

For all sets \(A\), \(B\), and \(C\):

\(\cup\) is idempotent: \(A\cup A=A\).
\(\cup\) is commutative: \(A\cup B= B\cup A\).
\(\cup\) is associative: \(A\cup(B\cup C)= (A\cup B)\cup C\).
\(A\subset B\) if and only if \(A\cup B=B\).
\(A\cup \emptyset=A\).
\(A\subset(A\cup B)\) and \(B\subset(A\cup B)\)
If \(A\subset B\) then \((A\cup C)\subset (B\cup C)\).
\((A\cup B)\subset C\) if and only if \(A\subset C\) and \(B\subset C\).

The proof of the statements follows almost immediately from the definition of the concepts ofequality of sets, subset, empty set, intersection, and union of sets.

Absorption laws For all sets \(A\) and \(B\):

\(A\cap(A\cup B)=A\).
\(A\cup(A\cap B)=A\).

The proof of the statements follows almost immediately from the definition of the concepts of equality of sets, subset, intersection and union of sets. It always comes down to proving the equality of two sets by showing that one set is a subset of the other set and vice versa.

Distributive laws For all sets \(A\), \(B\), and \(C\):

\(A\cap(B\cup C)=(A\cap B)\cup(A\cap C)\).
\(A\cup(B\cap C)=(A\cup B)\cap(A\cup C)\).

The proof of the statements follows almost immediately from the definition of the concepts equality of sets, subset, intersection and union of sets. It always comes down to proving the equality of two sets by showing that one set is a subset of the other set and vice versa.

Difference of sets and complement

Difference and complement

If \(A\) and \(B\) are sets, then the difference of A and B , denoted \(A\backslash B\), is the set of all elements that belong to \(A\) and not to \(B\). In formula form: \[A\backslash B=\{x \mid x\in A\text{ en } x\notin B\}\] If \(A\) is the universe \(U\) from which elements of \(B\) have been chosen, then we call \(U\backslash B\) the complement of \(B\) and we denote this as \(B^c\).

From the definition of difference it immediately follows that for every set \(A\) and the universe \(U\): \[\begin{aligned}A\backslash \emptyset &=A\\ A\backslash A &=\emptyset \\ \emptyset^{c}&=U\\ U^c&=\emptyset\end{aligned}\] .

Examples

\[\{1,2,3\}\backslash\{1,3,5\}=\{2\}\] \[[0,\infty)\backslash (-1, 1)=[1,\infty)\] \[\{1,2\}\backslash\{3,4\}=\{1,2\}\] If \(U=\mathbb{Z}\), then \[\{0\}^c=\{n\in \mathbb{Z}\mid n\neq 0\}\] If \(U=\mathbb{R}\), then \[\begin{aligned}(-1,1){}^{c} &=(-\infty,-1]\cup[1,\infty)\\ &=\{x \mid x\le -1\text{ of } x\ge 1\}\end{aligned}\]

Other notation for complement If \(A\) is a set, then its complement \(A^c\) is also notated as \(A'\) and as \(\overline{A}\).

Involution law for complement For every set \(A\), the following statement is true: \((A^c)^c=A\).

If \(A\) is a set within the universe \(U\), then: \[\begin{aligned}(A^c)^c &= \{x\in U\mid x\notin A^c\} \\ &= \{x\in U\mid x\in A\}\\ &= A\end{aligned}\]

The law of reciprocity For all sets \(A\) and \(B\), the following statement is true: \[A\subset B\text{ if and only if } A^c\supset B\,^c\text.\]

In words The law of reciprocity can also be formulated as follows: When changing to the complement, \(\subset\) and \(\supset\) are interchanged.

\(A\subset B\)
if and only if for every \(x\): if \(x\in A\), then \(x\in B\)
if and only if for every \(x\): if \(x\notin B\), then \(x\notin A\)
if and only if for every \(x\): if \(x\in B\,^c\), then \(x\in A^c\)
if and only if \(B\,^c\subset A^c\)
if and only if \(A^c\supset B\,^c\).

Rules of de Morgan For all sets \(A\) and \(B\): \[\begin{aligned} (A\cup B)^c&=A^c\cap B\,^c\\ (A\cap B)^c&=A^c\cup B\,^c\end{aligned}\]

In words The rules of de Morgan can also be formulated as follows: When changing to the complement, \(\cup\) and \(\cap\) are interchanged.

For sets \(A\) and \(B\) within the universe \(U\): \[\begin{aligned} (A\cup B)^c &=\{x\in U\mid x\notin(A\cup B)\}\\ &= \{x\in U\mid x\notin A\text{ and } x\notin B\}\\ &= \{x\in U\mid x\in A^c\text{ and } x\in B\,^c)\}\\ &= A^c \cap B\,^c\\ \\ (A\cap B)^c &= \{x\in U\mid x\notin(A\cap B)\}\\ &=\{x\in U\mid x\notin A\text{ or } x\notin B\}\\ &=\{x\in U\mid x\in A^c \text{ or } x\in B\,^c\}\\ &= A^c\cup B\,^c\end{aligned}\]

Symmetric difference of sets

Symmetric difference

The symmetric difference of two sets \(A\) and \(B\), denoted as \(A\triangle B\), is in formula form: \[A\triangle B=(A\backslash B)\cup(B\backslash A)\text.\] For non-disjoint sets, the Venn diagram below corresponds to this (see later in this section).

symmetrischverschil

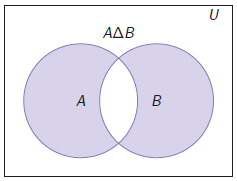
This Venn diagram also illustrates: \[\begin{aligned} A\triangle B&=(A\cup B)\backslash (A\cap B)\\[0.25cm] A\triangle B&=B\triangle A\end{aligned}\]

Examples

\[\begin{aligned}\{1,2\}\triangle \{2,3,4\}&=\{1,3,4\}\\[0.25cm] \{a,b,c\}\triangle \{b,c,d\} &= \{a,d\}\end{aligned}\]
For a set \(A\) the following applies: \[A\triangle A=\emptyset\;\text{ en }\;A\triangle \emptyset=A\]

Other notations For the symmetric difference \(A\triangle B\) of two sets \(A\) and \(B\), the following notations are also used: \[A\blacktriangle B\text{,}\quad A\otimes B\text{,} \quad A\oplus B\text.\]

For all sets \(A\), \(B\), and \(C\) the following statement is true: \[(A\triangle B)\triangle C=A\triangle (B\triangle C)\]