Naive set theory: Relations
 Basic concepts
Basic concepts
The Cartesian product \(X\times Y\) of sets \(X\) and \(Y\) is primarily introduced to define relations, of which functions are a special case.
Relation
Relation
A relation \(R\) from a set \(X\) to \(Y\) is a subset \(R\subset X\times Y\) of \(X\times Y\). If \((x,y)\) is an element of the relation \(R\), we also denote this as \(xRy\). If we want to emphasize that two sets are involved in a relation, we use the term binary relation.
A relation on \(X\) is a subset \(R \subset X\times X\).
Examples
Let \(X=\{1,2\}\text{, }Y=\{2,3,4\}\) and \(R=\{(1,2), (1,3),(2,2)\}\). Then \(R\) is a relation from \(X\) to \(Y\).
\(\{(x,y)\in \mathbb{R}\times\mathbb{R}\mid x<y\}\) is a relation on \(\mathbb{R}\).
\(\{(x,y)\in \mathbb{N}\times\mathbb{N}\mid y=x+1\}\) is a relation on \(\mathbb{N}\).
If \(X\) is a set, then \(\mathrm{Id}_X=\{(x,y)\in X^2\mid x=y\}\) is a relation, namely the identity relation on \(X\), also called the identity or diagonal on \(X\)
Domain and range of a binary relation
For a binary relation \(R\) from a set \(X\) to \(Y\), we define the domain \(\mathrm{dom}(R)\) and the codomain or range \(\mathrm{ran}(R)\) as \[\begin{aligned} \mathrm{dom}(R)&=\{x\in X\mid\text{ there exists some }y\in Y\text{ such that }xRy\}\\[0.25cm]\mathrm{ran}(R)&=\{y\in Y\mid\text{ there exists some }x\in X\text{ such that }xRy\}\end{aligned}\]
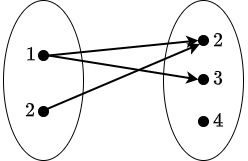
Let \(X=\{1,2\}\), \(Y=\{2,3,4\}\) and \(R=\{(1,2), (1,3),(2,2)\}\). Then \(R\) is a relation from \(X\) to \(Y\) and \[\begin{aligned} \mathrm{dom}(R)&=\{1,2\}\\[0.25cm]\mathrm{ran}(R)&=\{2,3\}\end{aligned}\] This relation can be represented graphically as follows:
Inverse relation
Inverse relation
For a binary relation \(R\) from a set \(X\) to \(Y\), we define the inverse relation \(R^{-1}\) as the set of ordered pairs \((y,x)\in Y\times X\) for which \((x,y)\in R\).
Example
If \(R=\bigl\{(x,y)\in \mathbb{R}\times \mathbb{R}\mid x<y\bigr\}\), then \(R=\bigl\{(x,y)\in \mathbb{R}\times \mathbb{R}\mid x>y\bigr\}\).
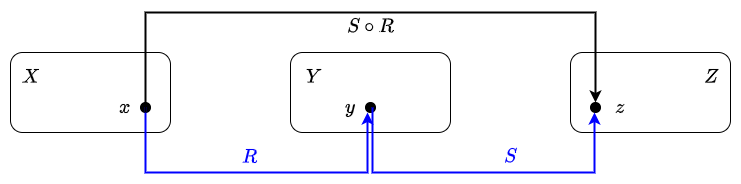
Composition of relations For a binary relation \(R\) from a set \(X\) to \(Y\) and a binary relation \(S\) from \(Y\) to a set \(Z\), we define the composition \(S\circ R\) of \(S\) and \(R\) as the set of ordered pairs \((x,z)\in X\times Z\) for which there exists a \(y\in Y\) such that \((x,y)\in R\) and \((y,z)\in S\).
Suppose \(R\) is a relation from \(X\) to \(Y\), \(S\) is a relation from \(Y\) to \(Z\), and \(T\) is a relation from \(Z\) to \(W\). Then:
- \((R^{-1})^{-1}=R\);
- \(\mathrm{dom}(R^{-1})=\mathrm{ran}(R)\);
- \(\mathrm{ran}(R^{-1})=\mathrm{dom}(R)\);
- \(T\circ(S\circ R)=(T\circ S)\circ R\);
- \((S\circ R)^{-1}=R^{-1}\circ S^{-1}\).


